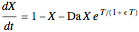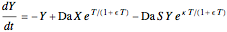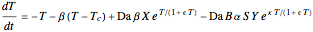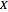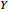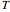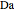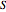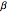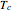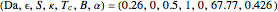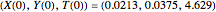Dynamics of a Continuous Stirred-Tank Reactor with Consecutive Exothermic and Endothermic Reactions
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
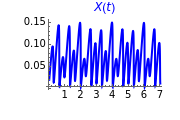
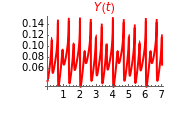
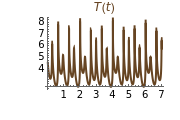
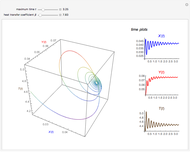
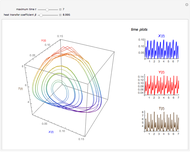
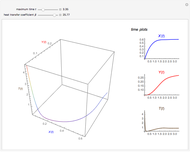
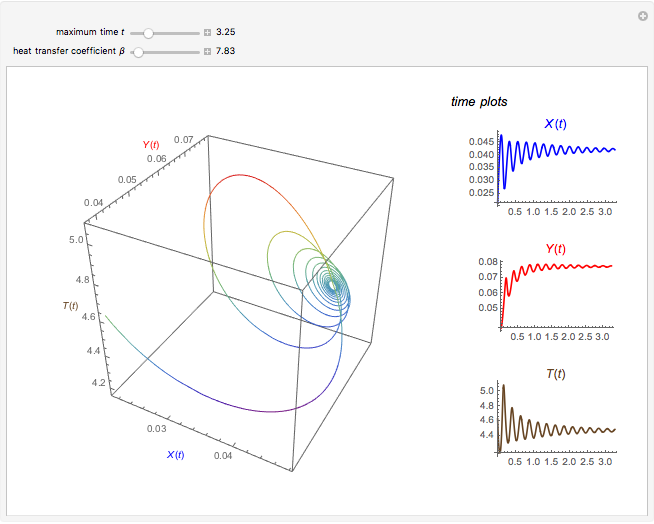
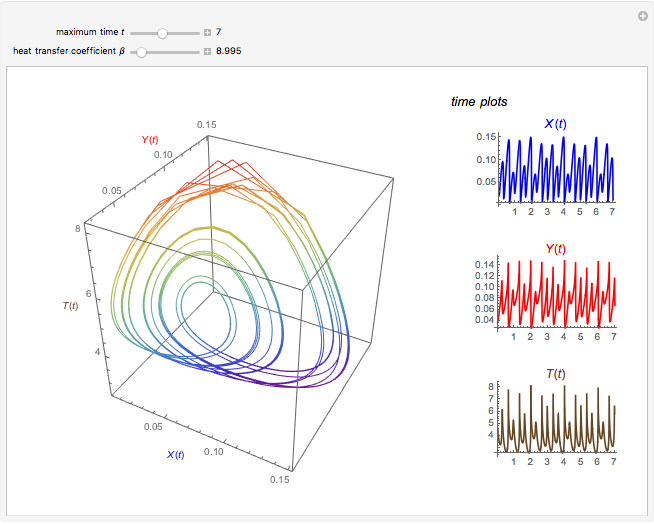
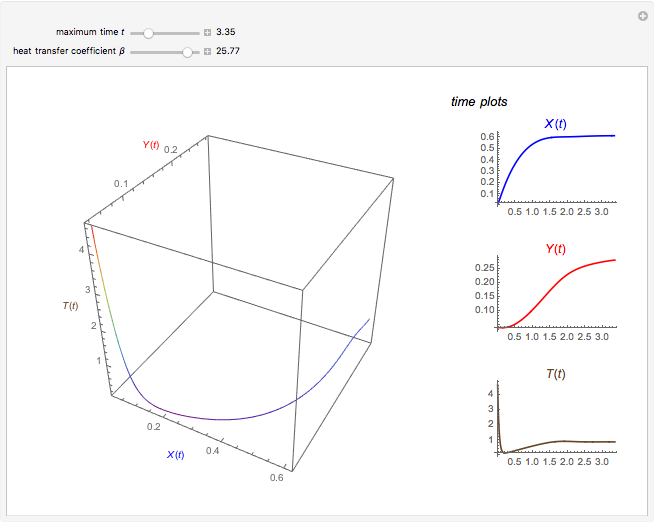
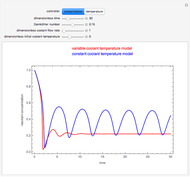
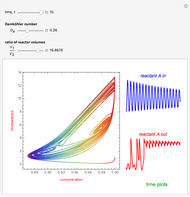
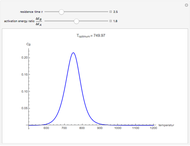
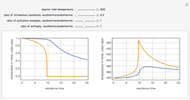
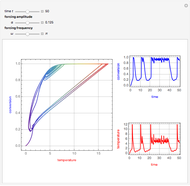
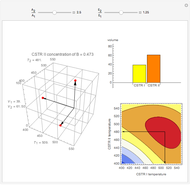
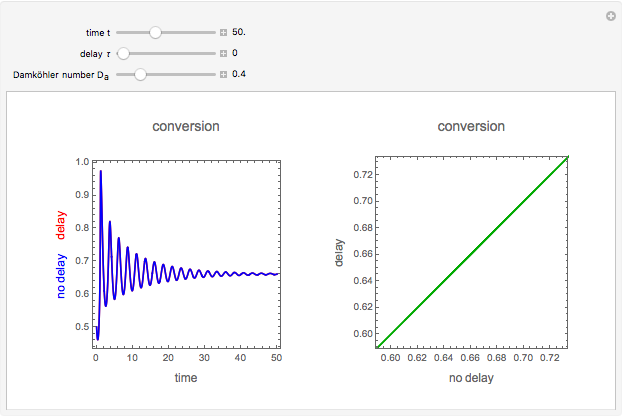
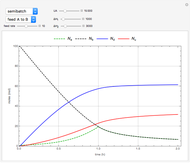
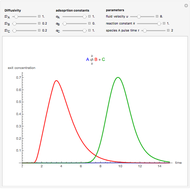
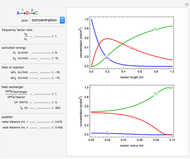
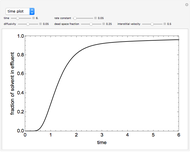
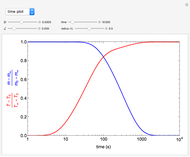
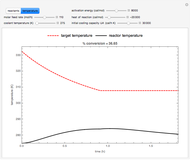
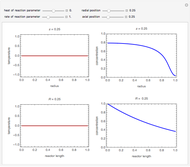
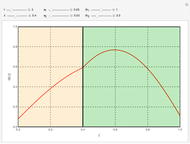
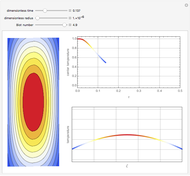
This Demonstration illustrates the dynamics of two irreversible consecutive reactions, 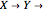 , the first exothermic, the second endothermic, in a continuous stirred-tank reactor. The dimensionless equations for this system [1] are
, the first exothermic, the second endothermic, in a continuous stirred-tank reactor. The dimensionless equations for this system [1] are
Contributed by: Clay Gruesbeck (November 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] C. Kalhert, O. E. Rössler, and A. Varma, "Chaos in a Continuous Stirred Tank Reactor with two Consecutive First Order Reactions, One Exo-, One Endothermic," Springer Series in Chemical Physics, 18, 1981 pp. 366–465.
Permanent Citation