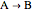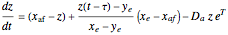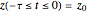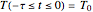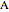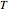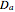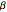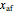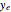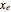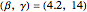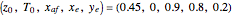Dynamics of a Coupled Reactor-Separator System with Time Delay

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
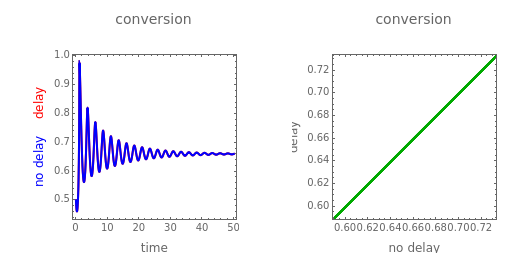
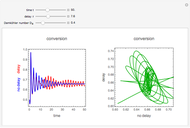
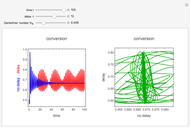
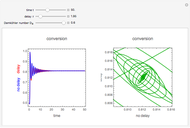
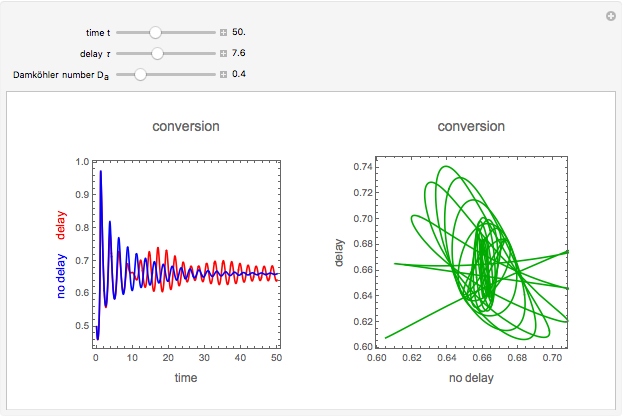
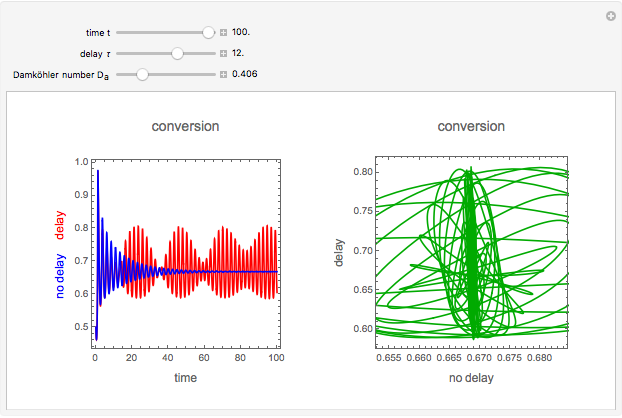
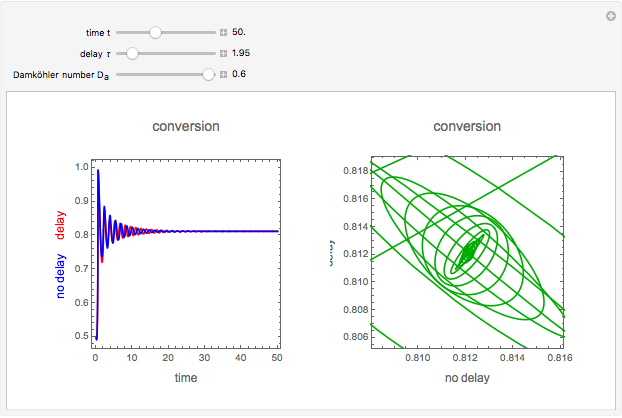
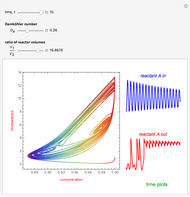
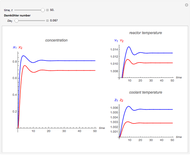
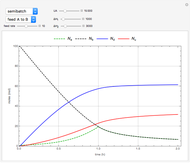
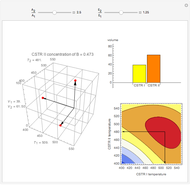
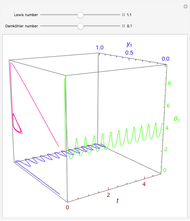
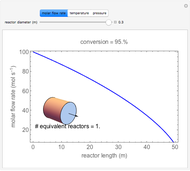
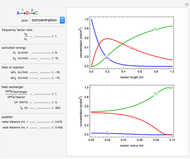
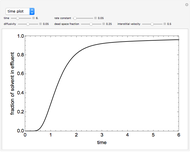
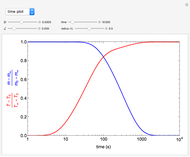
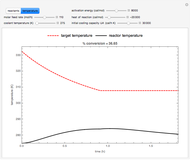
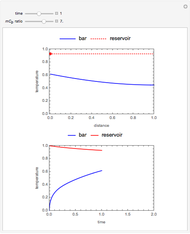
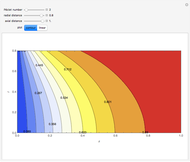
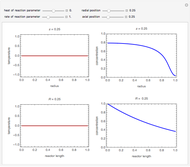
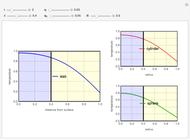
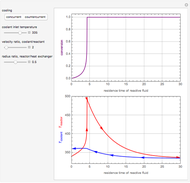
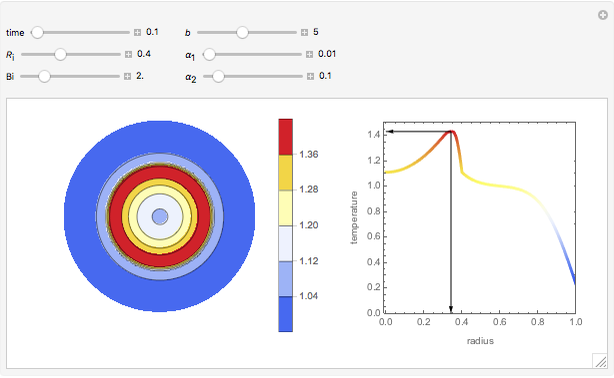
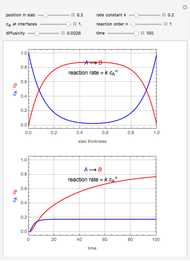
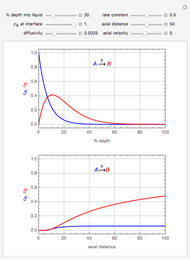
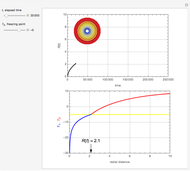
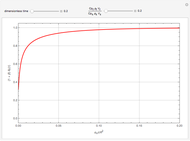
This Demonstration analyzes the effect of time delay on the behavior of a coupled non-isothermal continuous-flow stirred tank reactor (CSTR) with a separator.
[more]
Contributed by: Clay Gruesbeck (March 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] P. Balasubramanian, S. Pushpavanam, and A. Kienle, "Delay Effect in a Coupled Reactor-Separator System Sustaining Non Isothermal Reaction," Proceedings of the National Conference on Nonlinear Systems & Dynamics, Indian Institute of Technology, Kharagpur, India, Dec. 28–30, 2003 pp. 189–192. ncnsd.org/proceedings/proceeding03/html/pdf/189-192.pdf.
[2] Wikipedia. "Damköhler Numbers." (Feb 26, 2013) en.wikipedia.org/wiki/Damk% C3 % B6hler_numbers.
Permanent Citation