Periodic Quantum Motion of Two Particles in a 3D Harmonic Oscillator Potential

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
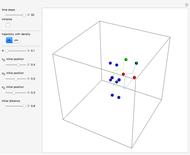
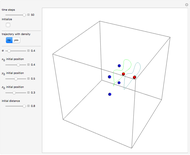
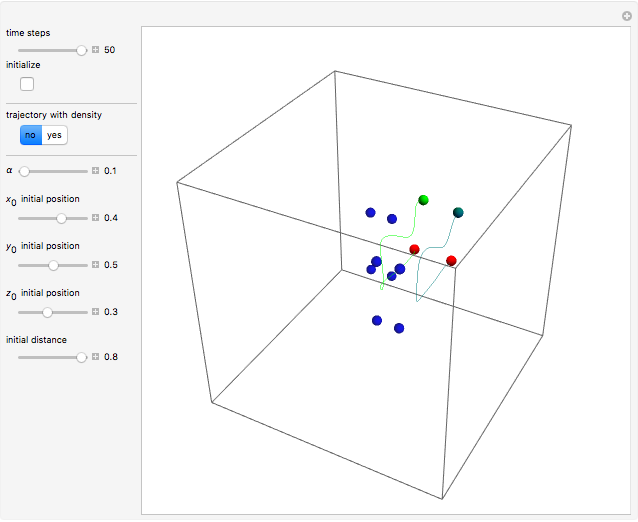
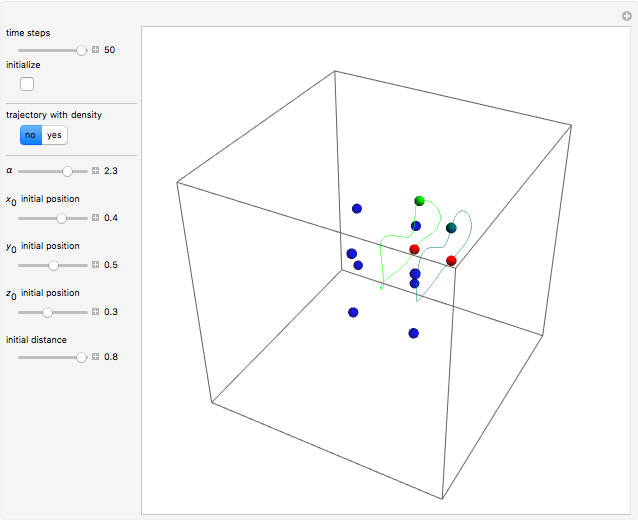
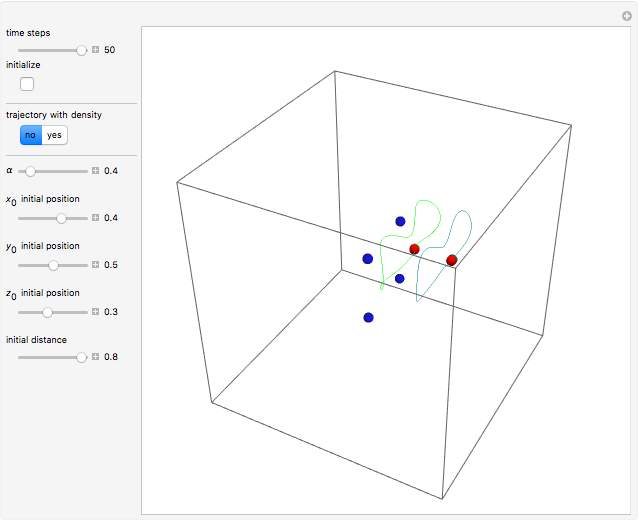
Bohmian quantum mechanics allows for both waves and particles, whereby particles are guided by the phase of the total wavefunction. The velocity of the particles becomes autonomous only with a periodic trajectory structure, when the corresponding wavefunction is in a degenerate stationary state of two eigenfunctions differing by a constant phase shift. This Demonstration studies the dynamic structure of the superposition of two three-dimensional eigenstates of the harmonic oscillator, which leads to periodic motion in configuration space. Two particles are placed on the margin of the harmonic potential randomly and separated by an initial distance 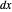 .
.
Contributed by: Klaus von Bloh (June 2015)
Open content licensed under CC BY-NC-SA
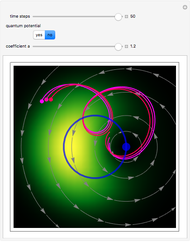
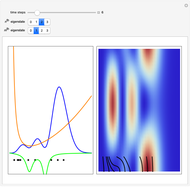
Snapshots
Details
Associated Hermite polynomials arise as the solution of the Schrödinger equation:
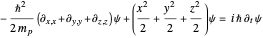 ,
with
,
with  ,
, 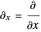 , and so on. A degenerate, unnormalized, complex-valued wavefunction
, and so on. A degenerate, unnormalized, complex-valued wavefunction 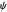 for the three-dimensional case can be expressed by:
for the three-dimensional case can be expressed by:
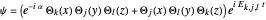 ,
,
where 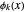 ,
, 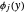 , and
, and 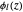 are eigenfunctions, and
are eigenfunctions, and 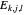 are permuted eigenvalues of the corresponding stationary one-dimensional Schrödinger equation with
are permuted eigenvalues of the corresponding stationary one-dimensional Schrödinger equation with  . The eigenfunctions are defined by:
. The eigenfunctions are defined by:
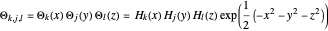 ,
,
where 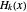 ,
, 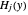 , and
, and 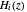 are Hermite polynomials. The parameter
are Hermite polynomials. The parameter 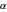 is a constant phase shift, and the energies depend on the quantum numbers, with
is a constant phase shift, and the energies depend on the quantum numbers, with 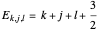 , with
, with  .
.
For this Demonstration, the wavefunction  is defined by:
is defined by:
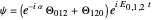 .
.
In this case, the square of the Schrödinger wavefunction 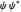 , where
, where  is its complex conjugate, is time independent:
is its complex conjugate, is time independent:
 .
.
The velocity field  is calculated from the gradient of the phase from the total wavefunction in the eikonal form (often called polar form)
is calculated from the gradient of the phase from the total wavefunction in the eikonal form (often called polar form)  . The time-dependent phase function
. The time-dependent phase function 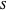 from the total wavefunction
from the total wavefunction 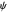 is:
is:
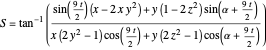 .
.
The corresponding velocity field becomes time independent (autonomous) because of the gradient of the phase function.
In the program, if PlotPoints, AccuracyGoal, PrecisionGoal, MaxSteps, and MaxIterations are enabled and increased, the results will be more accurate.
References
[1] "Bohmian-Mechanics.net." (June 10, 2015) www.bohmian-mechanics.net/index.html.
[2] S. Goldstein. "Bohmian Mechanics." The Stanford Encyclopedia of Philosophy. (June 10, 2015)plato.stanford.edu/entries/qm-bohm.
Permanent Citation