Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

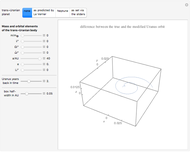
Simulating Real Gases in 2D

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

This Demonstration simulates the effects of intermolecular forces on the pressure and temperature of gas particles enclosed in a spherical container. The interparticle forces are constructed to have a finite range. The time-stepping algorithm that is employed takes advantage of this to reduce the time complexity, which for pairwise forces normally is 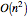, to the much more manageable .

[more]

In addition to pressure and temperature, you can see some derived thermodynamic quantities as functions of time, represented as curves. For closer inspection, you can select the time interval for display. Time-step selection is automatic. You can set container size to grow or shrink slowly and you can heat or cool the gas. You can switch the forces between particles from one type to another and vary their magnitude and sign.

The initial positions of the particles form a lattice such that the spheres of influence just touch. You control the lattice sites that are occupied by setting a probability. The initial velocities are set with random direction and an absolute value that gives the total system a selected temperature. This enumeration makes clear that many parameters can be set, allowing various kinds of observations being made. The detailed explanations of these parameters are given in the form of annotations that appear as you mouse over them. To read the annotations, you may need to pause the program by unchecking the run box.

[less]

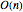Contributed by: Ulrich Mutze (December 2016)
Open content licensed under CC BY-NC-SA

Snapshots

Details

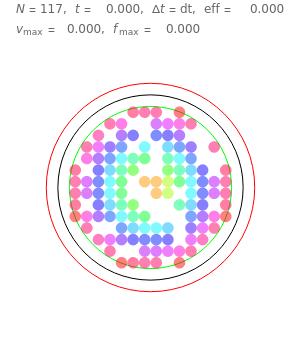
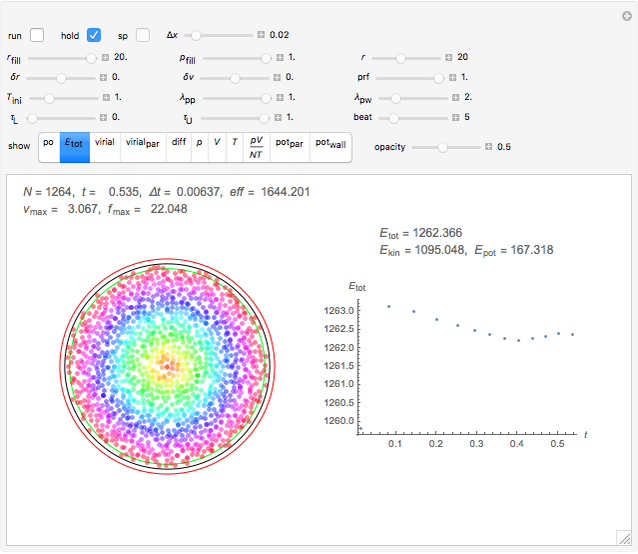
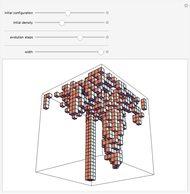
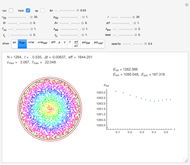
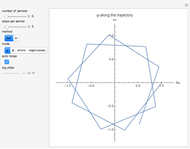
Snapshot 1: This is the system with the largest number of particles possible for this Demonstration. From the regularly packed initial configuration, a few integration steps were done. Notice the efficiency measure which, when compared with snapshots with fewer particles 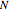, shows that the actual computation time per integration step grows even more slowly than .

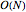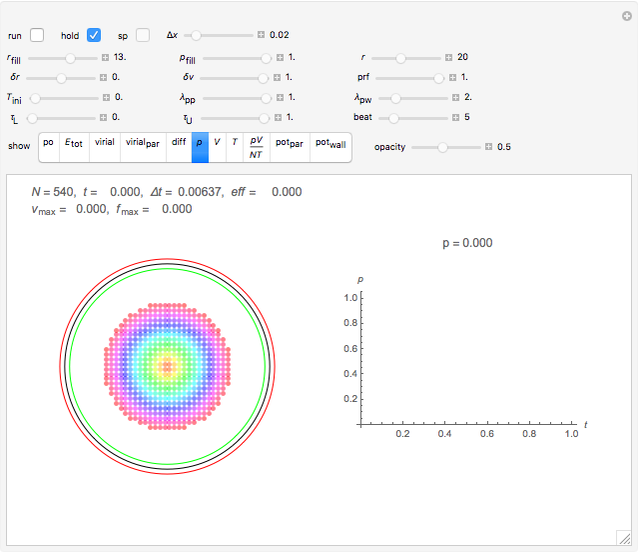
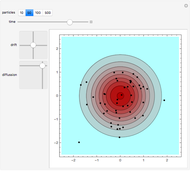
Snapshot 2: initial state of a compact system that will be heated and will evaporate as seen in the next snapshot

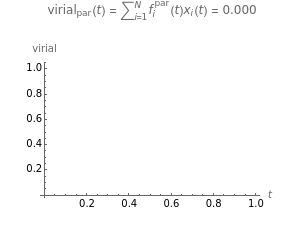
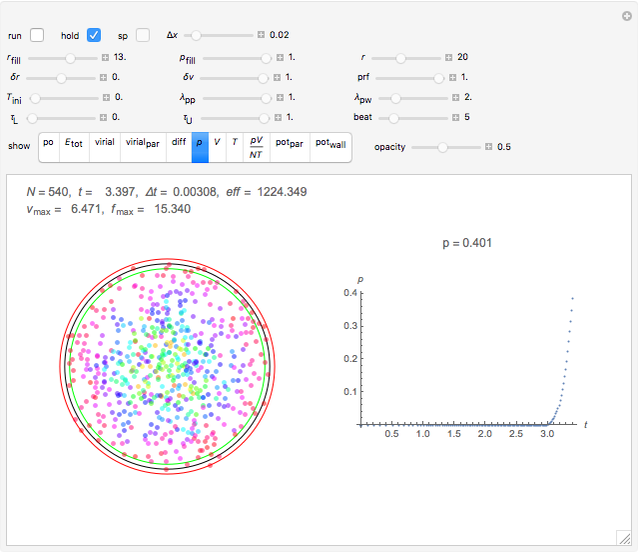
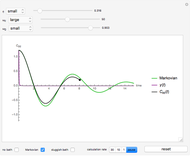
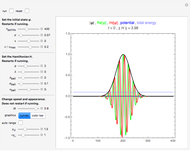
Snapshot 3: the pressure diagram shows that after some heating, particles arrive at the wall and exert forces on it

Snapshot 4: this shows the temperature growth during heating for the process shown in Snapshot 3

Snapshot 5: typical pressure fluctuations

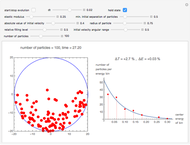
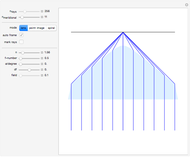
Snapshot 6: Deviation from the ideal gas equation of state for small particle-particle interaction. According to the ideal gas state equation (with the units used here and in 2D) ,the quantity shown here should oscillate around the value 1. The repulsive particle interaction shifts this to values larger than 1.

Snapshot 7: deviation from the ideal gas equation of state for 10-times-stronger particle-particle interaction

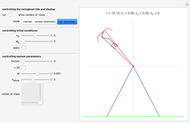
Snapshot 8: Condensation by cooling of binding particles in a wall-only container (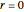). There are 25 particles that are distributed over nine positions.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send