Elliptical Torus

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
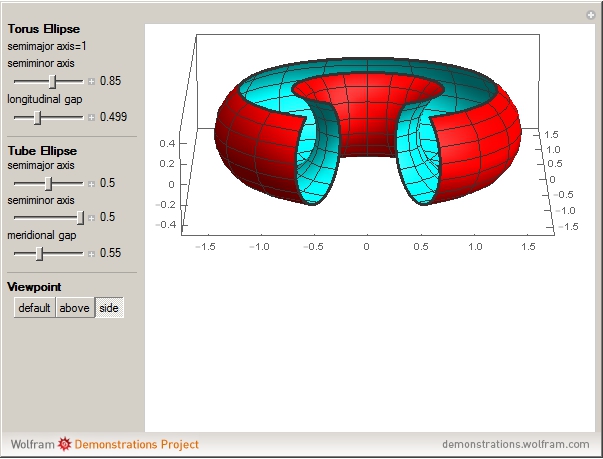
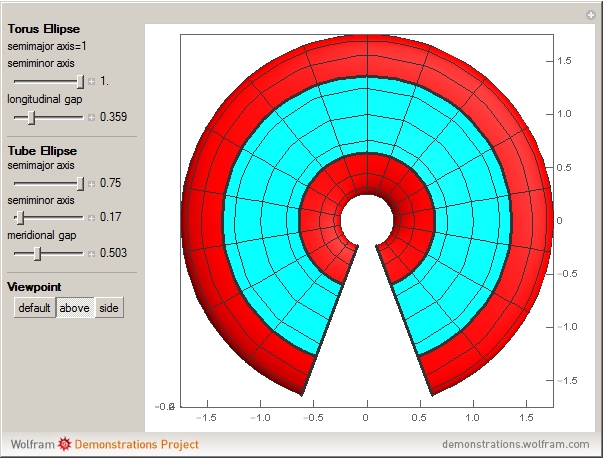
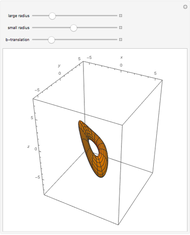
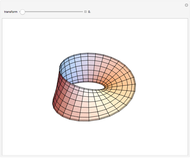
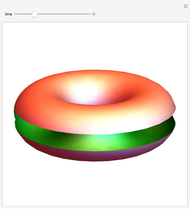
This Demonstration shows a torus for which both the tube and the cross section of the tube are elliptical.
[more]
Contributed by: Erik Mahieu (July 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The parametric equation of an elliptical ring torus with an elliptical cross section is obtained as follows.
The ring ellipse has parametric equation  in the
in the  -
-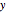 plane, where
plane, where 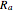 and
and  are the semimajor and semiminor axes.
are the semimajor and semiminor axes.
Using the Mathematica function FrenetSerretSystem, define the normal and binormal vectors 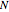 and
and 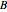 :
:
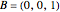 .
.
This gives the parametric equation of the elliptical torus:
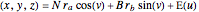 ,
,
where 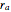 and
and 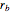 are the semimajor and semiminor axes of the cross-sectional ellipse.
are the semimajor and semiminor axes of the cross-sectional ellipse.
Expanded, this becomes:
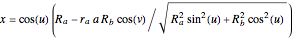 ,
,
 ,
,
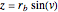 .
.
Permanent Citation