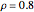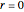Correlation and Regression Explorer

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
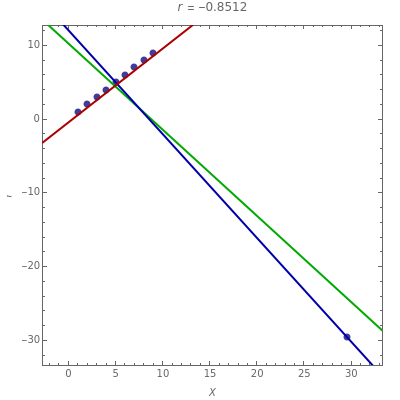
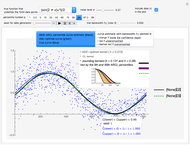
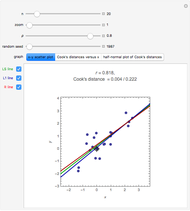
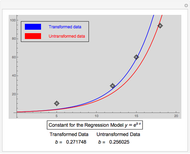
The scatter plot shown is based on an initial data configuration that was called Andrew's example in a lecture by J. W. Tukey that the author attended. Three types of regression lines are available: least squares (LS), least absolute deviation (L1), and a resistant line regression. See the Details section for more information about the regression lines. In Andrew's example, LS, L1, and RLINE all produce very different fits.
[more]
Contributed by: Ian McLeod (The University of Western Ontario) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
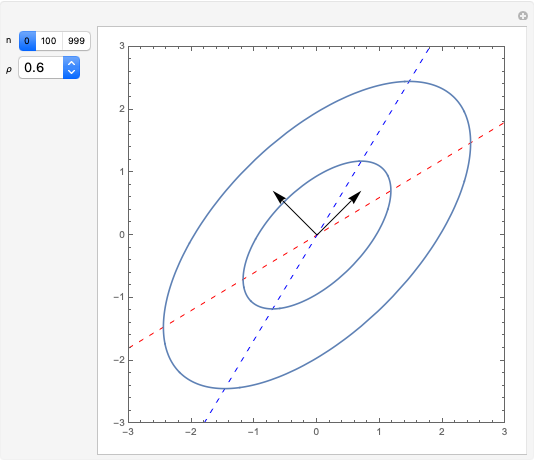
Snapshot 1: the points are similar to data generated from a bivariate normal distribution with correlation coefficient about 0.86
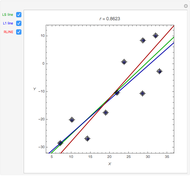
Snapshot 2: the data is the same as in snapshot 1 except a point has been added in the bottom-right corner; the LS regression line slope does not change much but the correlation does
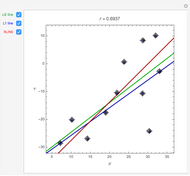
Snapshot 3: same as in snapshot 2 but the point is much further to the right; both correlation and regression lines have completely changed
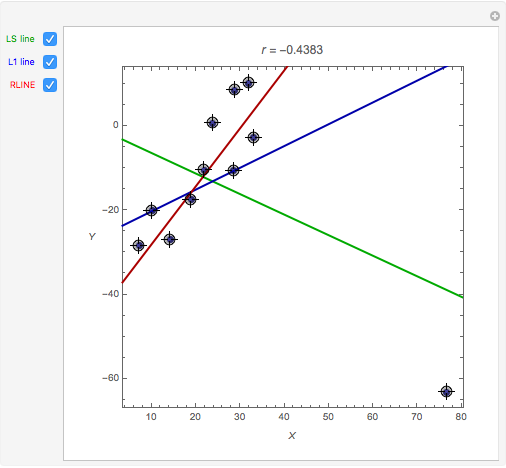
Snapshot 4: five points have been moved to roughly follow a parabolic curve; this illustrates that correlation does not measure nonlinear association
For LS regression, Mathematica's Fit function is used.
L1 regression minimizes the sum of absolute errors. This is computed using linear programming; see eqn. (3) in [2]. L1 regression is more robust than LS when moderate outliers are present, but it is still sensitive to extreme outliers.
RLINE: resistant regression line §5 [3] is based on medians.
[1] F. J. Anscombe, "Graphs in Statistical Analysis," The American Statistician, 27(2), 1973 pp. 17–21.
[2] S. C. Narula and J. F. Wellington, "The Minimum Sum of Absolute Errors Regression: A State of the Art Survey," International Statistical Review, 50(2), 1982 pp. 317–326.
[3] P. F. Velleman and D. C. Hoaglin, Applications, Basics and Computing of Exploratory Data Analysis, Boston: Duxbury Press, 1981.
Permanent Citation