Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Gray and Dark Solitons in the de Broglie and Bohm Approaches

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

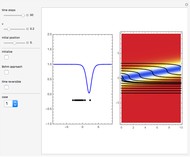
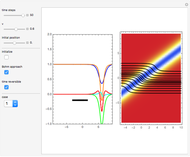
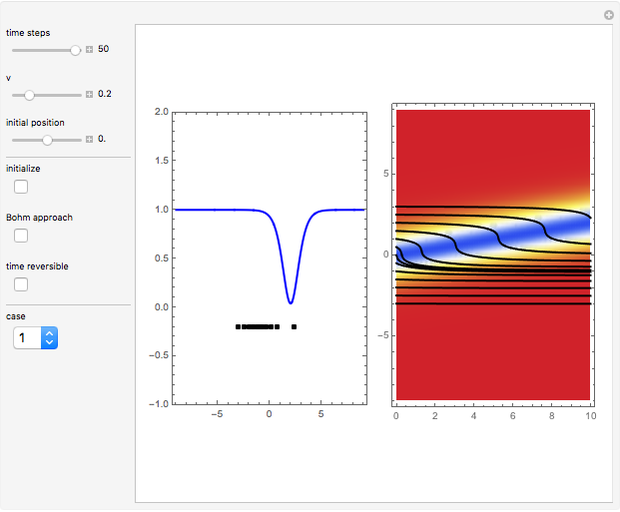
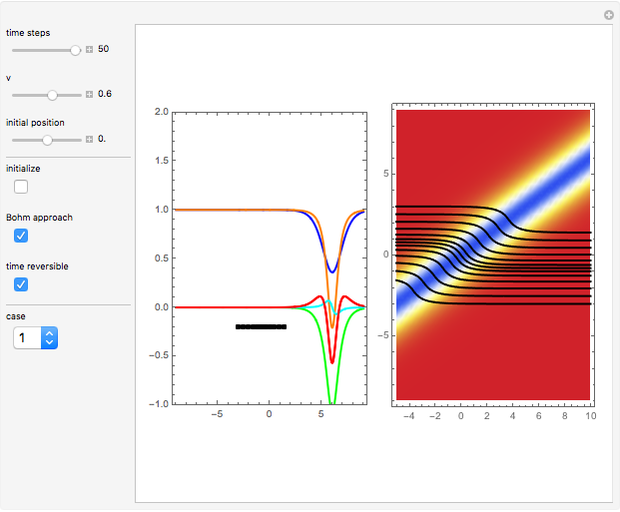
This Demonstration studies dark and gray types of solitons. Solitons are solutions of the one-dimensional nonlinear Schrödinger equation (NLS); they play an important role in the context of nonlocal nonlinear media (e.g fiber optics). In general, solitons are spatially localized waves propagating without changing their shape. A dark soliton has the form of a localized dip on a plane-wave background. In the de Broglie approach of quantum dynamics, the propagation of point-particles could be described by trajectories that are guided by the imaginary part of 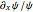for the pilot wave . In Bohm's approach (often called causal interpretation), there is a particle and a wave, too, but the wave creates a quantum potential, which generates a force on this particle. The quantum force for the NLS is defined by (a second-order differential equation in respect to time), where the effective potential is given by 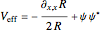, and where the quantum amplitude 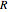is 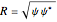, with acceleration and mass (here 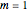). The first term of the effective potential is called the quantum potential; the second term describes the potential of a nonlinear amplitude depending medium.

[more]

For case 1, the particles stand still in the media. If a gray soliton propagates through this media, the particles are accelerated until the wave has left the region where the particles are positioned. After the interaction, the particles become motionless again, but their positions have shifted.

For case 2, the wave density of the dark solitons leads to a linear motion in - space. If the motion for case 2 is calculated by the quantum force (Bohm approach), there is a free parameter for the initial velocity because of the integration constant. If the initial velocity is to be , then both approaches are equal.

In the case of a gray soliton, the particles are attracted by the “dark density” region. The gray soliton could be interpreted as a perturbation of the particles in a nonlinear media. The amplitude of gray soliton determines the velocity of the minimum of the wave packet as other solitons do. The system is time reversible.

In the de Broglie approach, there is only the wave density (the pilot wave) and the particle position. In the Bohm approach, when the button is enabled, you see the quantum potential (red), the velocity (green), the effective potential (orange, the sum of quantum potential and wave density/potential), and the acceleration field (cyan) of the wave density. The acceleration field is scaled to fit.

[less]

Contributed by: Klaus von Bloh (September 2014)
Open content licensed under CC BY-NC-SA

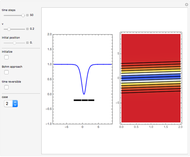
Snapshots

Details

Both types of solitons obey the nonlinear Schrödinger (NLS) equation:

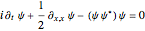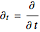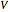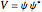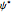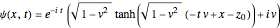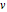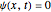, with and so on, also known as the Gross–Pitaevskii equation, where the nonlinear media is described by the potential with ( is the complex conjugate wave). The well-known exact solutions are complex fields of functions of and . For case 1, the wave is , where is the wave number with (if , then ) and 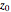gives the initial wave density minimum at . For case 2, the complex-valued wave is 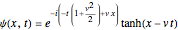, with wave number .

The velocity 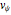, which governs the motion of the particles in configuration space, is determined by . For case 2, the velocity 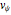is given by the wave number .

The effective potential 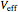for this case becomes a constant value (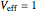), because the quantum potential cancels out the wave potential, from which the velocity could be calculated via the quantum force easily. For 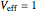, the acceleration 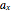of the particles, which is induced by the gradient of the effective potential 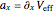, is zero. From the acceleration, the motion is obtained by integrating twice.

If the wave number becomes zero, the particles become motionless for both cases. The exact solutions are adapted and taken from [3].

References

[1] Bohmian-Mechanics.net. (Aug 12, 2014) www.bohmian-mechanics.net.

[2] S. Goldstein. "Bohmian Mechanics." The Stanford Encyclopedia of Philosophy. (Aug 12, 2014) plato.stanford.edu/entries/qm-bohm.

[3] Y.S. Kivshar and B. Luther-Davies, "Dark Optical Solitons: Physics and Applications," Physics Reports, 298, 1998 pp. 81–197.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send