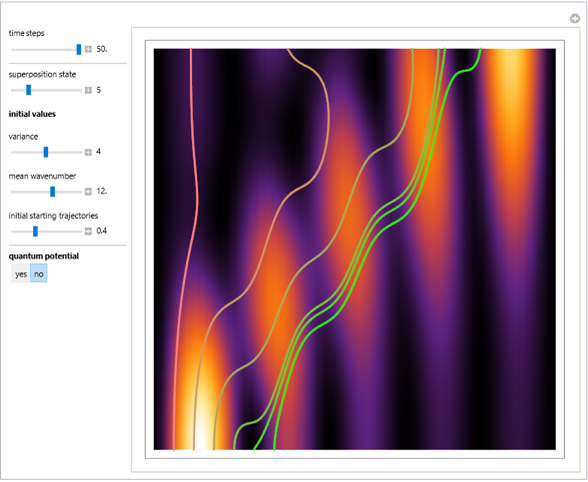
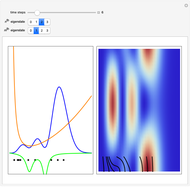
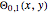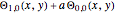Perturbation Theory in the de Broglie-Bohm Interpretation of Quantum Mechanics

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
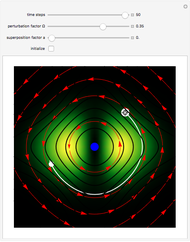
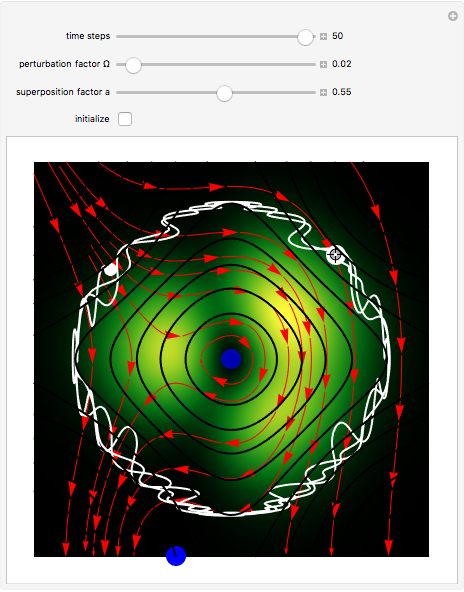
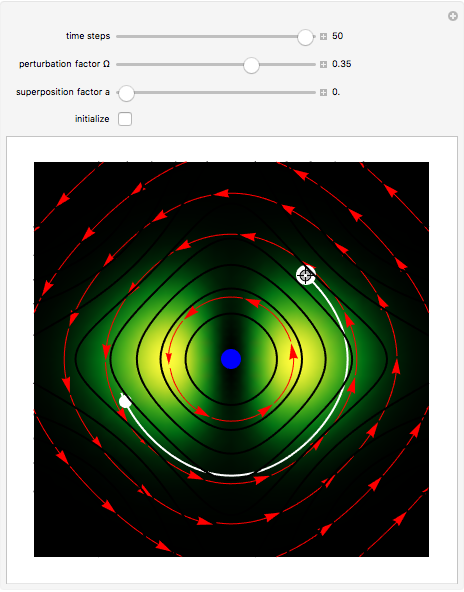
In the de Broglie–Bohm interpretation of quantum mechanics, the particle position and momentum are well defined, and the transition can be described as a continuous evolution of the quantum particle according to the time-dependent Schrödinger equation. There are no "quantum jumps." To study transitions in a two-level system, time-dependent perturbation theory must be used. These solutions are not exact solutions of the Schrödinger equation, but they are extremely accurate. For the particular case of a two-level system perturbed by a periodic external field (but without quantization of the transition-inducing field and ignoring radiation effects), an accurate solution can be derived (see Related Links).
[more]
Contributed by:Klaus von Bloh (July 2015)
Open content licensed under CC BY-NC-SA
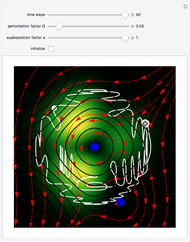
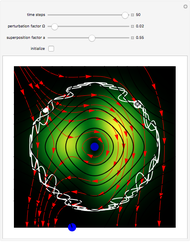
Snapshots
Details
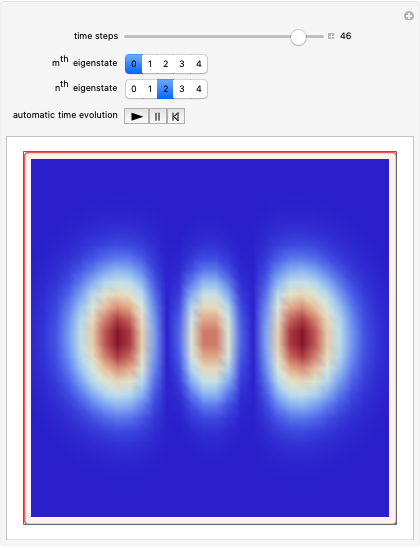
Associated Legendre polynomials arise as the solution of the Schrödinger equation
 ,
with
,
with 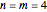 ,
, 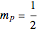 ,
, 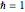 ,
,  , and so on. A degenerate, unnormalized wavefunction for the two-dimensional perturbed case, which leads to a transition from the state
, and so on. A degenerate, unnormalized wavefunction for the two-dimensional perturbed case, which leads to a transition from the state 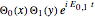 to the state
to the state 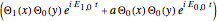 , can be expressed by
, can be expressed by
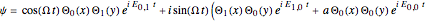 ,
,
where 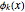 ,
, 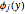 are eigenfunctions, and
are eigenfunctions, and  are permuted eigenenergies of the corresponding stationary one-dimensional Schrödinger equation, with
are permuted eigenenergies of the corresponding stationary one-dimensional Schrödinger equation, with 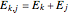 and
and  . In the wavefunction
. In the wavefunction  , the perturbation term is given by
, the perturbation term is given by 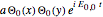 , where the parameter
, where the parameter  is an arbitrary constant. The eigenfunctions
is an arbitrary constant. The eigenfunctions 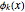 ,
, 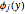 are defined by
are defined by
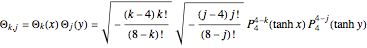 ,
,
where 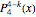 ,
, 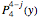 are associated Legendre polynomials.
are associated Legendre polynomials.  are the quantum numbers
are the quantum numbers 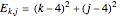 with
with 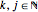 and
and 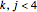 . The wavefunction is taken from [3].
. The wavefunction is taken from [3].
For  , the velocity field obeys the time-independent part of the continuity equation
, the velocity field obeys the time-independent part of the continuity equation 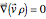 with
with 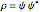 , where
, where 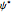 is the complex conjugate. For this special case (
is the complex conjugate. For this special case ( ), the trajectory becomes strongly periodic, because of the sign changing for
), the trajectory becomes strongly periodic, because of the sign changing for 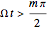 with
with  of the velocity term.
of the velocity term.
In the program, if PlotPoints, AccuracyGoal, PrecisionGoal, and MaxSteps are increased (if enabled), the results will be more accurate.
References
[1] C. Dewdney and M. M. Lam, "What Happens during a Quantum Transition?," Information Dynamics (H. Atmanspacher and H. Scheingraber, eds.), New York: Plenum Press, 1991.
[2] C. Efthymiopoulos, C. Kalapotharakos, and G. Contopoulos, "Origin of Chaos near Critical Points of the Quantum Flow," Physical Review E, 79, 2009 036203. doi:10.1103/PhysRevE.79.036203, arXiv:0903.2655 [quant-ph].
[3] M. Trott, The Mathematica GuideBook for Symbolics, New York: Springer, 2006.
[4] G. Pöschl and E. Teller, "Bemerkungen zur Quantenmechanik des anharmonischen Oszillators," Zeitschrift für Physik, 83 (3–4), 1933 pp. 143–151, doi:10.1007/BF01331132.
[5] "Bohmian-Mechanics.net." (Jul 30, 2015) www.bohmian-mechanics.net/index.html.
[6] S. Goldstein. "Bohmian Mechanics." The Stanford Encyclopedia of Philosophy. (Jul 30, 2015)plato.stanford.edu/entries/qm-bohm.
Permanent Citation