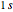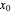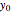Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Bohm Trajectories in an LCAO Approximation for the Hydrogen Molecule

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

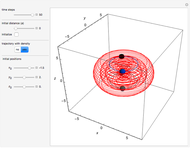
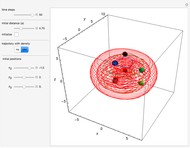
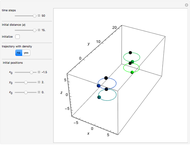
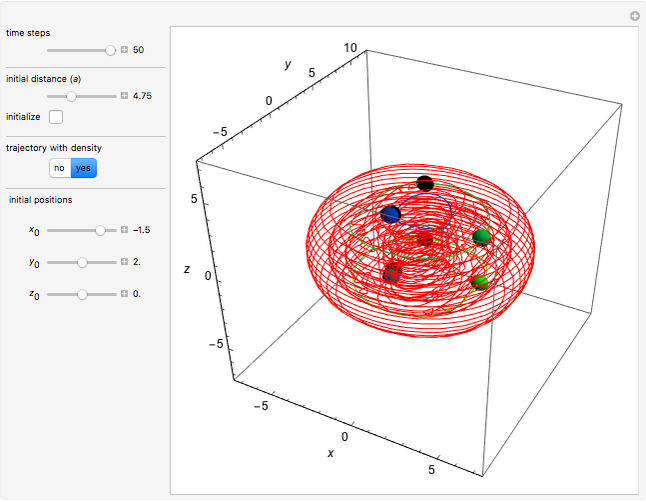
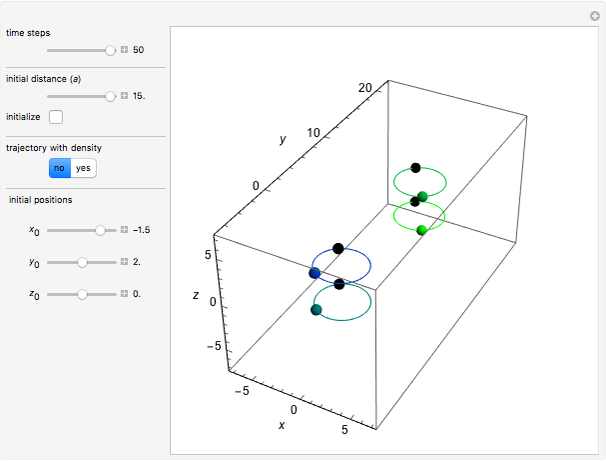
In quantum chemistry, linear combinations of atomic orbitals (LCAO) have long been used to construct molecular orbitals. This Demonstration considers the Bohm trajectories of two initially separated excited metastable hydrogen atoms, separated by an internuclear distance . Keep in mind that in this special case, the standard LCAO method must be adjusted to fit, and it does not give exact solutions to the Schrödinger equation, but only first approximations.

[more]

The most stable electronic state of an atom is called the ground state. An excited atom, which is called a Rydberg atom (with a very high principal quantum number ), in which the electron is not in the lowest-energy orbit, immediately emits energy in the form of light when the electron falls back into lower-energy orbit. Metastable states are excited atoms with a long lifetime before they return to the ground state by emitting photons.

An example of a metastable atom with a lifetime of about 0.12 seconds is the () excited state of the hydrogen atom, which undergoes radiative decay to the ground state (), only by two-photon transitions [6].

As in standard treatments of the hydrogen atom, the nuclei are assumed to have infinite mass and thus remain stationary in space, with the specified internuclear distance parameter in the direction. Thus the model consists of electrons that are electrostatically attracted to the stationary protons. This approximation neglects the kinetic energy of the nuclei, and the system is approximated as two separate one-electron molecular orbitals. In the Bohm picture, the electron acts like an actual particle, its velocity at any instant being fully determined by the gradient of the phase function, which in turn depends on the LCAO representation of the total molecular wavefunction. Dewdney and Malik [1], Holland [2] and Colijn and Vrscay [3] first examined the Bohmian trajectories associated with eigenstates for the hydrogen atom.

Pauli's exclusion principle, which states that two identical electrons cannot occupy the same spin-orbital within a quantum system, plays no role here since the two occupied molecular orbitals of the hydrogen molecule have opposite spins. There are four possible Bohm trajectories for two electrons in depending on the initial position , , and the internuclear distance parameter . If , you see only one electron with two possible orbits. In the interference region of the two hydrogen atoms, the component of the velocity is not equal to zero.

In the graphic you see the wave density (if enabled); four possible orbits of two electrons, where one trajectory (blue) depends on the initial starting point (, , ), and the initial starting points of the four trajectories (black points, shown as small spheres) and the actual position (colored points, shown as small spheres).

[less]

Contributed by: Klaus von Bloh (December 2017)
Open content licensed under CC BY-NC-SA

Snapshots

Details

With the internuclear distance parameter 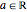, since the Coulomb potential

.

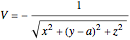
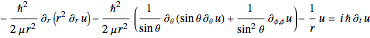For simplicity, set the reduced mass and equal to 1 (atomic units). This leads to the time-dependent wavefunction with the associated Laguerre polynomials 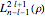and the spherical harmonics :

,

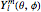with the energy eigenvalue 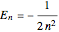and 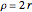. The principal quantum number determines the energy, 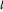is called the orbital angular momentum quantum number and is the magnetic quantum number. To get Bohm trajectories, the hydrogen atom has to be excited because the magnetic number must be 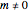, which is only fulfilled for states with 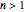. When , the electron is at rest; for a stationary state with 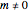, the electron orbits the axis along a circle of constant radius and with constant angular speed, depending on the sign and magnitude of [2].

For ( 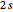state), the energy equals 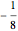. For , , , 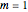in Cartesian coordinates with

,

,

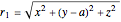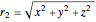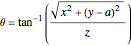and

,

the spatial wavefunction on each of the two hydrogen atoms forms a linear combination that leads to LCAO-MO-like application to 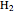, which is not the standard LCAO-MO method, with:

.

For this very special case, the wavefunction becomes:

.

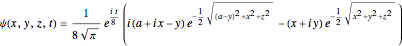For , the wavefunction becomes an exact solution of the Schrödinger equation. From the wavefunction for , the equation for the phase function follows:

In Cartesian coordinates, the 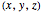components of the velocity could be declared by the gradient of the total phase function from the total wave function in the eikonal form, which lead in this special case to a corresponding autonomous differential equation system:

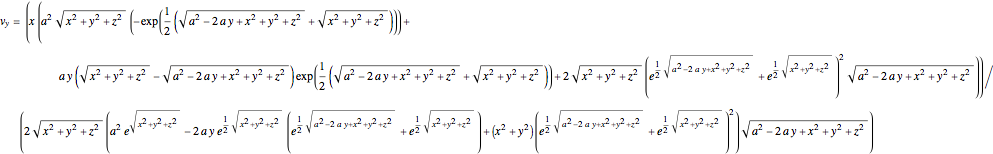
and

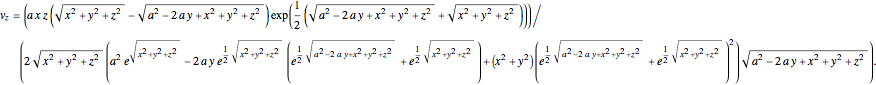
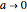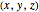For the limiting case and for the asymptotic behavior , the components of the velocity become:

,

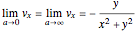and

.

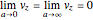For more detailed information about the hydrogen-like atom and Bohm theory, see [1–3, 6, 7], and for a general introduction to Bohmian mechanics, see [2, 4, 5].

In the program, to make the results more accurate, increase PlotPoints, MaxRecursion, AccuracyGoal, PrecisionGoal and MaxSteps.

References

[1] C. Dewdney and Z. Malik, "Angular-Momentum Measurement and Nonlocality in Bohm’s Interpretation of Quantum Theory," Physical Review A, 48(5), 1993 pp. 3513–3524. doi:10.1103/PhysRevA.48.3513.

[2] P. Holland, The Quantum Theory of Motion: An Account of the de Broglie–Bohm Causal Interpretation of Quantum Mechanics, Cambridge: Cambridge University Press, 1993.

[3] C. Colijn and E. R. Vrscay, "Spin-Dependent Bohm Trajectories for Hydrogen Eigenstates," Physics Letters A, 300(4–5), 2002 pp. 334–340. doi:10.1016/S0375-9601(02)00824-1.

[4] "Bohmian-Mechanics.net." (Dec 20, 2017) www.bohmian-mechanics.net/index.html.

[5] S. Goldstein. "Bohmian Mechanics." The Stanford Encyclopedia of Philosophy. (Dec 20, 2017)plato.stanford.edu/entries/qm-bohm.

[6] L. P. Yatsenko, V. I. Romanenko, B. W. Shore, T. Halfmann and K. Bergmann,"Two-Photon Excitation of the Metastable 2s State of Hydrogen Assisted by Laser-Induced Chirped Stark Shifts and Continuum Structure," Physical Review A, 71(3), 2005 pp. 1–10. doi:10.1103/PhysRevA.71.033418.

[7] Wikipedia. "Hydrogen Atom." (Dec 20, 2017) en.wikipedia.org/wiki/Hydrogen_atom.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send