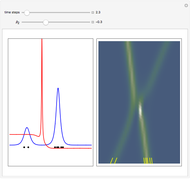
Decoherence and Trajectories Implied by a Modified Schrodinger Equation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Decoherence is defined as the emergence of classical behavior through interaction of a quantum system with the environment. It is the most widely accepted explanation of how quantum systems become classical. For other points of view, see, for example, [1, 2]. Interference of coherent superposition of quantum amplitudes  ,
, 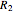 in Young's double-slit experiment is a preeminent feature of quantum systems, but in the classical limit, the interference term vanishes. Classical behavior is exhibited in the trajectories of the particles when each particle goes through one slit and is not affected by the other slit.
in Young's double-slit experiment is a preeminent feature of quantum systems, but in the classical limit, the interference term vanishes. Classical behavior is exhibited in the trajectories of the particles when each particle goes through one slit and is not affected by the other slit.
Contributed by: Partha Ghose and Klaus von Bloh (July 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The initial wavefunction in the eikonal form,
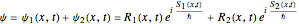 ,
,
obeys the free-particle Schrödinger equation in the  direction:
direction:
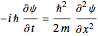 ,
,
here with 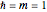 . The initial wavefunction is a linear combination of two Gaussian packets with initial spatial half-widths
. The initial wavefunction is a linear combination of two Gaussian packets with initial spatial half-widths  and group velocities
and group velocities  . The measured intensity
. The measured intensity 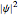 at any time
at any time  is given by
is given by
 .
.
According to the theory proposed in [1], the measured intensity 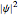 takes the form
takes the form
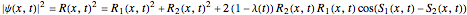 ,
,
with 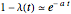 and
and  , where
, where  is the coherence time, a measurement of how fast the system becomes classical. For simplicity,
is the coherence time, a measurement of how fast the system becomes classical. For simplicity,  is called the decoherence coupling factor. In this context, classical means that the probability density
is called the decoherence coupling factor. In this context, classical means that the probability density  becomes
becomes
 .
.
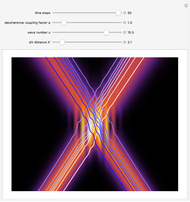
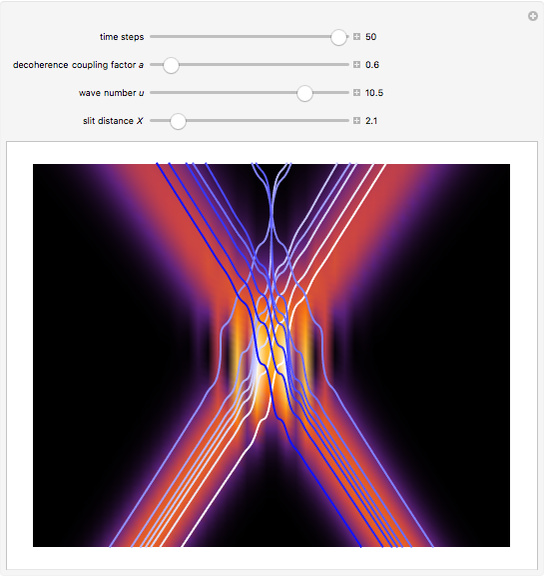
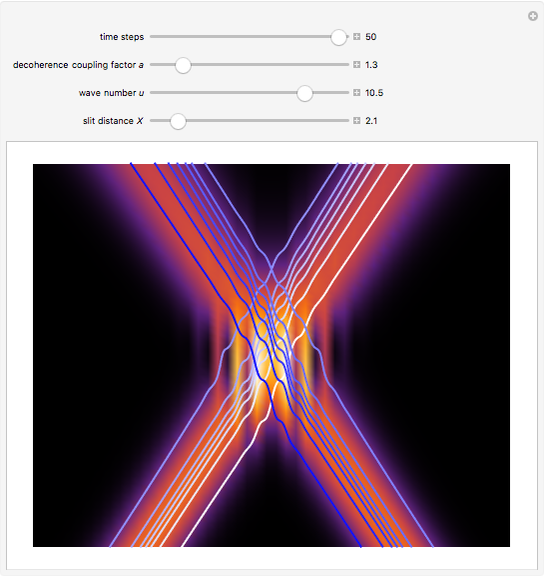
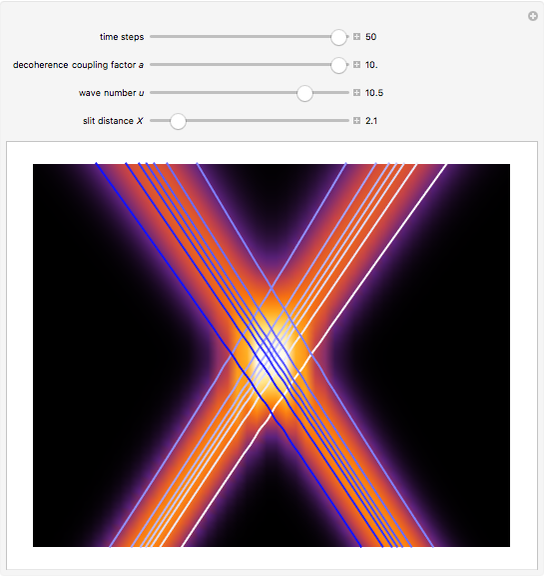
If  (the quantum limit), there is full coherence with
(the quantum limit), there is full coherence with 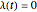 and there is no difference between the general Bohm view and the quantum potential approach. The trajectories run to the local maxima of the squared wavefunction and therefore correspond to the bright fringes of the diffraction pattern. The quantum particle passes through slit one or slit two and never crosses the axis of symmetry.
and there is no difference between the general Bohm view and the quantum potential approach. The trajectories run to the local maxima of the squared wavefunction and therefore correspond to the bright fringes of the diffraction pattern. The quantum particle passes through slit one or slit two and never crosses the axis of symmetry.
For unit mass 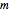 , the general equation of motion is given by the acceleration term that is the second derivative of the position
, the general equation of motion is given by the acceleration term that is the second derivative of the position 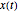 with respect to time
with respect to time  :
:
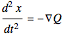 ,
,
where 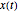 is integrated numerically for various initial positions and velocities. The initial positions are linearly distributed around the peaks of the wave. The initial velocities are taken from the gradient of the phase function for
is integrated numerically for various initial positions and velocities. The initial positions are linearly distributed around the peaks of the wave. The initial velocities are taken from the gradient of the phase function for  . The quantum potential
. The quantum potential 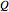 , from which the trajectories are calculated, is given by:
, from which the trajectories are calculated, is given by:
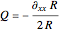 ,
,
with
 .
.
For  the coupling function
the coupling function 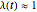 , the effect of the quantum potential
, the effect of the quantum potential 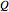 vanishes, and there is no dependence of the trajectories on the phase functions
vanishes, and there is no dependence of the trajectories on the phase functions 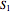 and
and 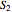 . This leads to the crossing of trajectories.
. This leads to the crossing of trajectories.
The results become more accurate if you increase AccuracyGoal, PrecisionGoal and MaxSteps.
For more detailed information about Bohmian mechanics, see [5, 6], and for an animated example describing a similar situation, see [7].
References
[1] P. Ghose, "Continuous Quantum-Classical Transitions and Measurement: A Relook." arxiv.org/abs/1705.09149v1.
[2] P. Ghose and K. von Bloh, "Continuous Transitions between Quantum and Classical Motions." arxiv.org/abs/1608.07963.
[3] A. S. Sanz and F. Borondo, "A Quantum Trajectory Description of Decoherence," The European Physical Journal D, 44(2), 2007 pp. 319–326. doi:10.1140/epjd/e2007-00191-8.
[4] B.-G. Englert, M. O. Scully, G. Süssman and H. Walther, "Surrealistic Bohm Trajectories," Zeitschrift für Naturforschung, 47(12), 1992 pp. 1175–1186. doi:10.1515/zna-1992-1201.
[5] "Bohmian-Mechanics.net." (Jun 29, 2017) www.bohmian-mechanics.net/index.html.
[6] S. Goldstein. "Bohmian Mechanics." The Stanford Encyclopedia of Philosophy. (Jun 29, 2017)plato.stanford.edu/entries/qm-bohm.
[7] P. Ghose and K. von Bloh. Decoherence and Crossing Trajectories in the de Broglie–Bohm Approach [Video]. (Jul 3, 2017), www.youtube.com/watch?v=ONw5SHIRe-0.
Permanent Citation