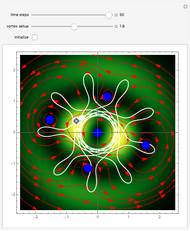
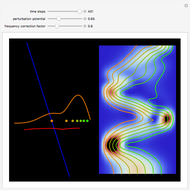
The Which-Way Experiment and the Conditional Wavefunction

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
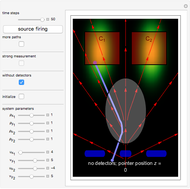
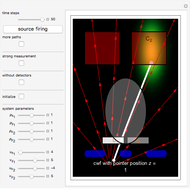
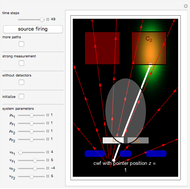
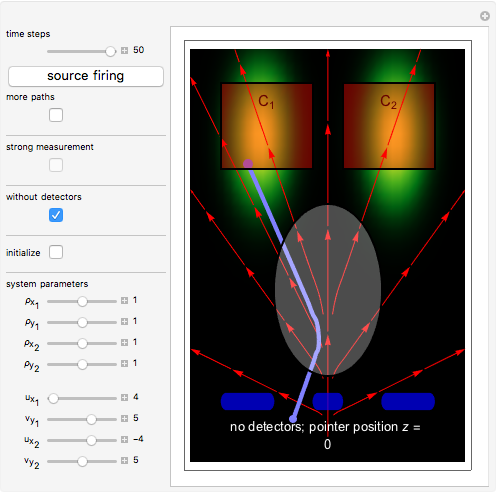
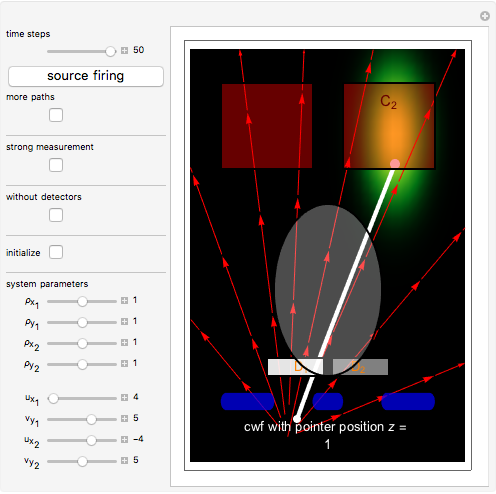
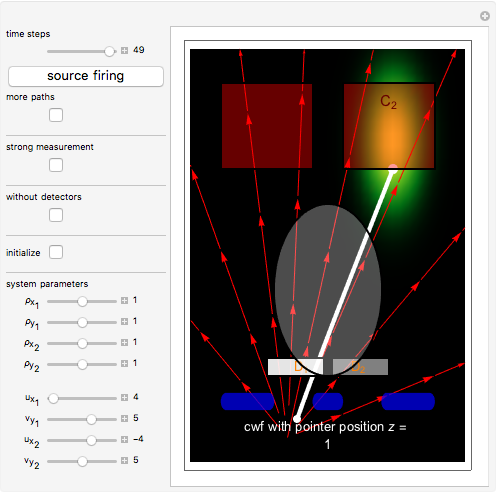
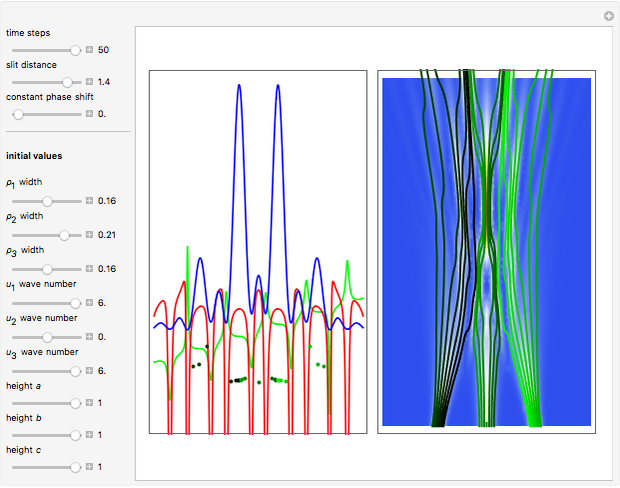
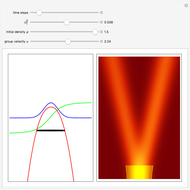
In a which-way experiment, a beam of quantum point-like particles, emitted by a narrow source of width  , is divided into two partial beams by a double slit. A beam is represented mathematically by a two-dimensional Gaussian wave packet (with negligible dispersion), constructed so that the beams can interfere. If no position-measuring device is placed in the apparatus, you can observe an interference phenomenon in region I (the gray area), which could be described mathematically as a superposition of the wavefunctions from the two arms. Suppose next that two detectors are added to the setup just behind slits 1 and 2 to register the passage of a particle.
, is divided into two partial beams by a double slit. A beam is represented mathematically by a two-dimensional Gaussian wave packet (with negligible dispersion), constructed so that the beams can interfere. If no position-measuring device is placed in the apparatus, you can observe an interference phenomenon in region I (the gray area), which could be described mathematically as a superposition of the wavefunctions from the two arms. Suppose next that two detectors are added to the setup just behind slits 1 and 2 to register the passage of a particle.
Contributed by: Klaus von Bloh (October 2015)
After suggestion by: Detlef Dürr
After work by: John Stewart Bell
Open content licensed under CC BY-NC-SA
Snapshots
Details
Without the detectors, the total wavefunction is the superposition of the Gaussian profiles (unnormalized) in  configuration-space, where the time evolution is to be calculated from the free-particle Schrödinger equation. If the detectors
configuration-space, where the time evolution is to be calculated from the free-particle Schrödinger equation. If the detectors 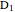 and
and 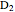 are added to the setup, the general solution
are added to the setup, the general solution  of the many-body Schrödinger equation yields a superposition of two entangled wavefunctions in the
of the many-body Schrödinger equation yields a superposition of two entangled wavefunctions in the 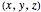 configuration-space
configuration-space
 , with
, with 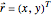 ,
,
where the  are two Gaussian profiles, and where
are two Gaussian profiles, and where 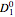 ,
, 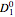 and
and 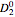 ,
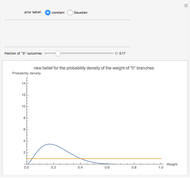
, 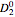 are wavefunctions for the position-recording detectors. The initial starting points are chosen randomly. For the strong measurement, the initial starting points are fixed (
are wavefunctions for the position-recording detectors. The initial starting points are chosen randomly. For the strong measurement, the initial starting points are fixed (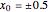 ).
).
In general, the wavefunction for the detectors is time-dependent, with complex dependence on many variables. But, in the case discussed, the many-body unnormalized wavefunction for the detectors simplifies so that it depends only on the time-independent variable  . Here
. Here 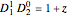 and
and 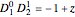 , where
, where  is the pointer position, which is the connection between the measurement device and the isolated quantum system. In the CI approach the initial position of the particle from which the path is calculated defines the pointer position
is the pointer position, which is the connection between the measurement device and the isolated quantum system. In the CI approach the initial position of the particle from which the path is calculated defines the pointer position  .
.
In our case the cwf is defined as the wavefunction  , evaluated for special values of
, evaluated for special values of  . For
. For 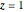 (strong measurement: detector
(strong measurement: detector 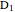 recorded the position and counter
recorded the position and counter 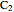 is registering) and for
is registering) and for  (strong measurement: detector
(strong measurement: detector 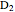 recorded the position and counter
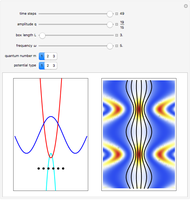
recorded the position and counter 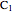 is registering), there is no interference, no empty wave, and the particle obeys the naive perception of reality. If
is registering), there is no interference, no empty wave, and the particle obeys the naive perception of reality. If 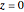 , then the detectors are removed and the quantum system is isolated from the rest of the world. The counters always register the particles coming from the wrong slit. For
, then the detectors are removed and the quantum system is isolated from the rest of the world. The counters always register the particles coming from the wrong slit. For 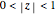 , the quantum system and the measurement device are weakly connected and interference still occurs. In this case particles can take paths that contradict the naive perception of reality.
, the quantum system and the measurement device are weakly connected and interference still occurs. In this case particles can take paths that contradict the naive perception of reality.
For more detailed information about Bohmian mechanics, see [4–7].
The author would like to thank Detlef Dürr for helpful discussions.
References:
[1] J. S. Bell, "De Broglie–Bohm, Delayed-Choice, Double-Slit Experiment, and Density Matrix," International Journal of Quantum Chemistry: Quantum Chemistry Symposium, 18(S14), 1980 pp. 155–159. doi:10.1002/qua.560180819.
[2] B.-G. Englert, M. O. Scully, G. Süssman, and H. Walther, "Surrealistic Bohm Trajectories," Zeitschrift für Naturforschung, 47(12), 1992 pp. 1175–1186.
[3] C. Dewdney, L. Hardy, and E. J. Squires, "How Late Measurements of Quantum Trajectories Can Fool a Detector," Physics Letters A, 184(1), 1993 pp. 6–11. doi:10.1016/0375-9601(93)90337-Y.
[4] P. Holland, The Quantum Theory of Motion, Cambridge: Cambridge University Press, 1995.
[5] S. Goldstein, "Bohmian Mechanics," The Stanford Encyclopedia of Philosophy. (Sep 30, 2015)plato.stanford.edu/entries/qm-bohm.
[6] Bohmian-Mechanics.net. (Sep 30, 2015) www.bohmian-mechanics.net/index.html.
[7] D. Dürr, S. Goldstein, and N. Zanghí, "Quantum Equilibrium and the Origin of Absolute Uncertainty," Journal of Statistical Physics, 67(5), 1992 pp. 843–907. arXiv: 0308039 [quant-ph].
[8] S. Kocsis, B. Braverman, S. Ravets, M. J. Stevens, R. P. Mirin, L. Krister Shalm, and A. M. Steinberg, "Observing the Average Trajectories of Single Photons in a Two-Slit Interferometer," Science, 332(6034), 2011 pp. 1179–1173. doi:10.1126/science.1202218.
[9] T. Norsen and W. Struyve, "Weak Measurement and (Bohmian) Conditional Wave Functions," Annals of Physics, 350, 2014 pp. 166–178. arXiv:1305.2409v2 [quant-ph].
Permanent Citation