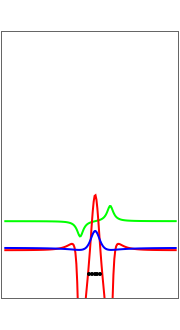
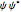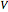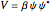Causal Interpretation of the Nonlinear Schrödinger Equation: An Analytic Example

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
The "self-focusing" nonlinear Schrödinger equation  with
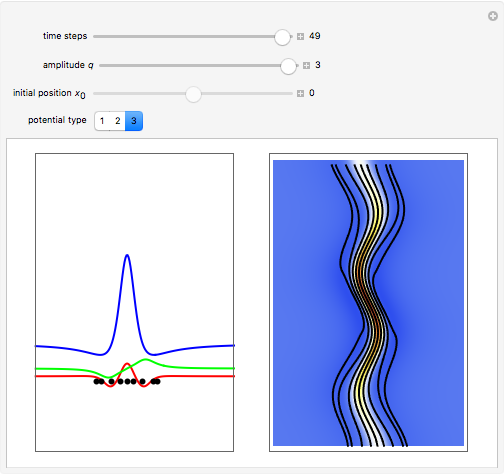
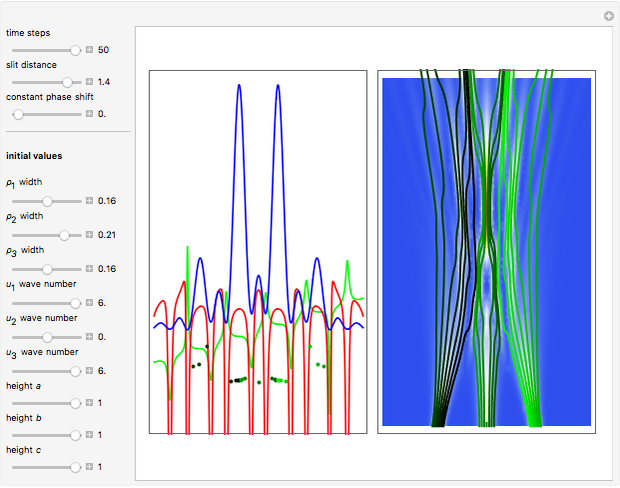
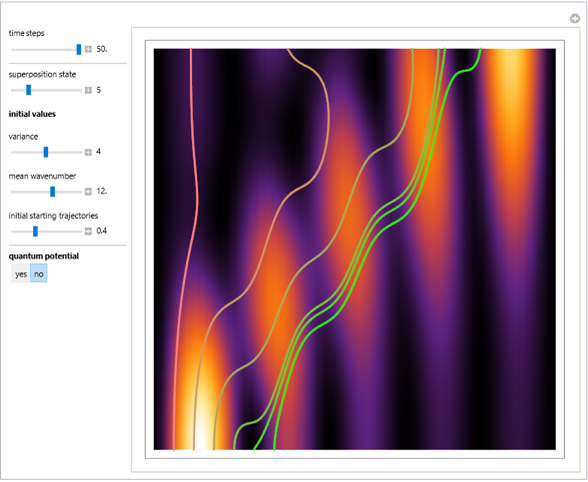
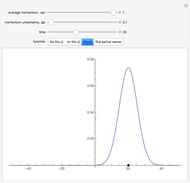
with 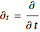 , and so on, also known as the Gross–Pitaevskii equation, appears in wave propagation in nonlinear media such as signal transmission in optical fibers, Bose–Einstein condensation, and surface waves over sufficiently deep water. In addition, this model plays a major role in the theory of rogue waves. After the Korteweg–de Vries equation, this was the second nonlinear partial differential equation whose initial value problem was solved via the inverse scattering transform method. It has two types of solutions, one associated with a group of waves and the other in which the velocity depends on the amplitude. The first is a soliton whose envelope does not change in form over time. The second family of solutions are the so-called "breathers", which are rational solutions of the nonlinear Schrödinger equation.
, and so on, also known as the Gross–Pitaevskii equation, appears in wave propagation in nonlinear media such as signal transmission in optical fibers, Bose–Einstein condensation, and surface waves over sufficiently deep water. In addition, this model plays a major role in the theory of rogue waves. After the Korteweg–de Vries equation, this was the second nonlinear partial differential equation whose initial value problem was solved via the inverse scattering transform method. It has two types of solutions, one associated with a group of waves and the other in which the velocity depends on the amplitude. The first is a soliton whose envelope does not change in form over time. The second family of solutions are the so-called "breathers", which are rational solutions of the nonlinear Schrödinger equation.
Contributed by: Klaus von Bloh (March 2011)
Open content licensed under CC BY-NC-SA
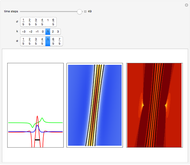
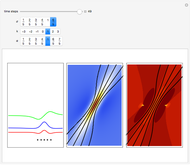
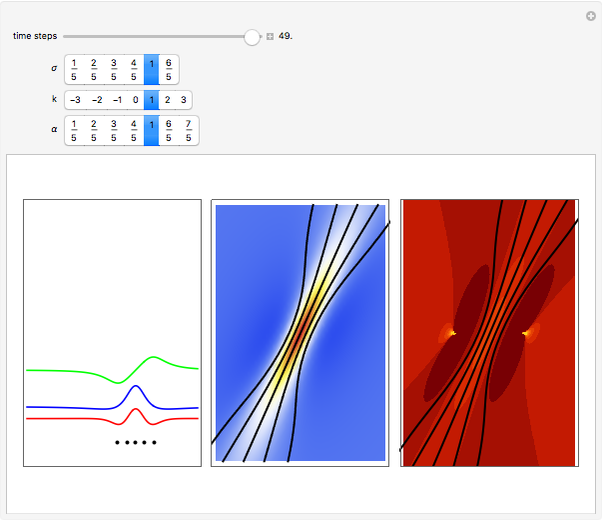
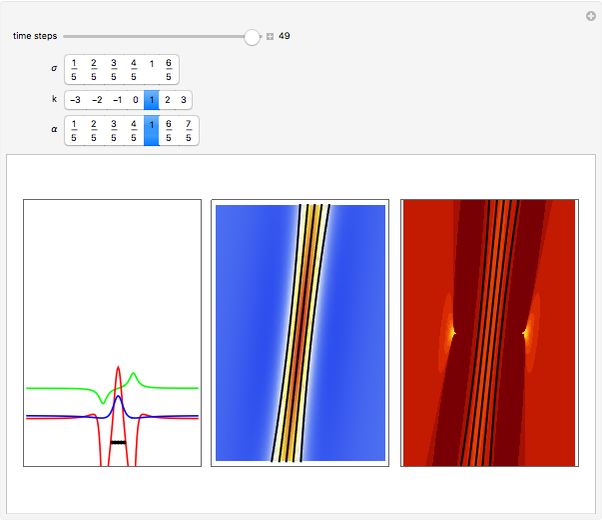
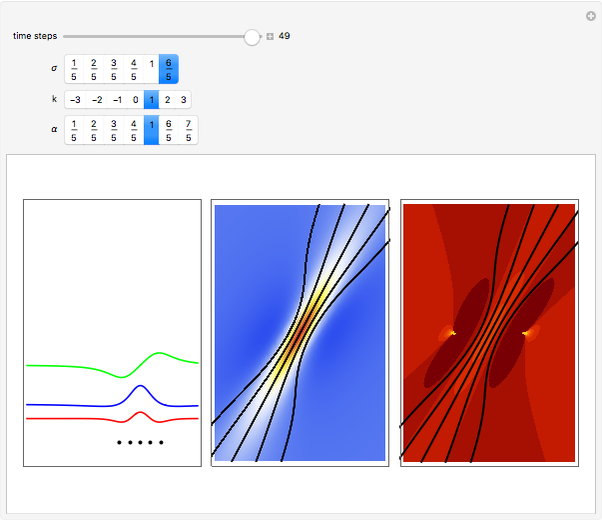
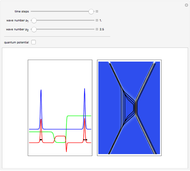
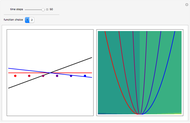
Snapshots
Details
For the complex wavefunction,  , where
, where  ,
,  ,
, 
 (initial width and amplitude) and
(initial width and amplitude) and  (wavenumber) are real-valued constants. The analytic solution for the trajectories is taken from [1]. For
(wavenumber) are real-valued constants. The analytic solution for the trajectories is taken from [1]. For  ,
,  , and
, and  the wavefunction
the wavefunction  turns into the Peregrine soliton
turns into the Peregrine soliton 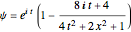 [2]. In the causal interpretation, only a few equations of motion are analytically integrable. In this Demonstration the equation of motion is derived by solving:
[2]. In the causal interpretation, only a few equations of motion are analytically integrable. In this Demonstration the equation of motion is derived by solving: 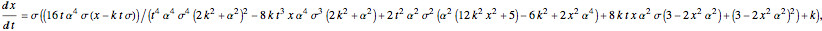
The analytical solution is given, and where  is an integration constant. The initial position is estimated by solving the equation
is an integration constant. The initial position is estimated by solving the equation  numerically. Real-valued trajectories are obtained for several
numerically. Real-valued trajectories are obtained for several  's. The path
's. The path  together with the starting point
together with the starting point 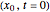 , lead to a trajectory in
, lead to a trajectory in  space, which is not the real
space, which is not the real 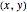 configuration space.
configuration space.
References
[1] Z. Yan, "Financial Rogue Waves," arXiv:0911.4259v2 [q-fin.PR], 2010.
[2] D. H. Peregrine, "Water Waves, Nonlinear Schrödinger Equations and Their Solutions," Journal of the Australian Mathematical Society, Ser. B, 25, 1983 pp. 16–43.
Permanent Citation