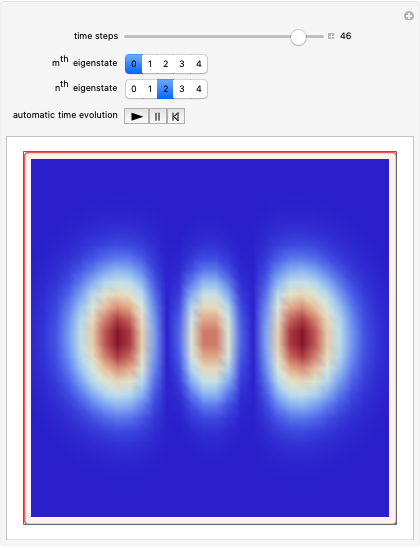
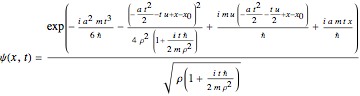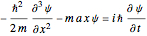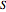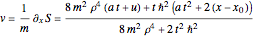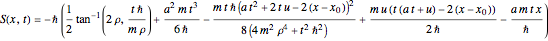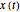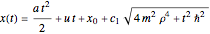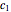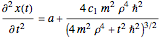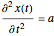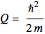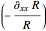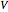This Demonstration studies a free-falling quantum particle with mass 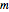 in a uniform gravitational potential
in a uniform gravitational potential 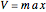 (in the Earth's gravitational field:
(in the Earth's gravitational field: 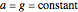 ). The equations of motion can be solved analytically for the classical and quantum-mechanical case. For the classical (i.e., Newtonian) case, the force is
). The equations of motion can be solved analytically for the classical and quantum-mechanical case. For the classical (i.e., Newtonian) case, the force is 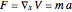 , which leads to the kinematic equation of motion:
, which leads to the kinematic equation of motion: 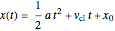 with constant acceleration
with constant acceleration  , constant initial velocity
, constant initial velocity 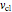 , and initial position
, and initial position 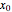 . Classically, the kinematic equation is independent of the mass, which shows that all bodies with different masses fall with an equal acceleration
. Classically, the kinematic equation is independent of the mass, which shows that all bodies with different masses fall with an equal acceleration  . In the quantum case the time-evolution of the wavefunction for an initial Gaussian packet (initial maximum
. In the quantum case the time-evolution of the wavefunction for an initial Gaussian packet (initial maximum 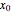 , group velocity
, group velocity  , initial density
, initial density  , mass
, mass 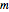 ) in a uniform field with the strength
) in a uniform field with the strength  is described by a complex-valued field:
is described by a complex-valued field:
[more]
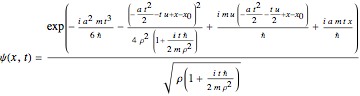 , satisfying Schrödinger’s wave equation
, satisfying Schrödinger’s wave equation 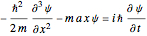 (here
(here  ). The center of the packet accelerates in the direction
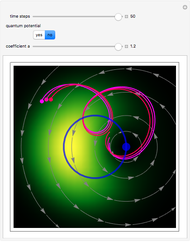
). The center of the packet accelerates in the direction  . Bohm's causal interpretation (today often called the de Broglie-Bohm interpretation) of non-relativistic quantum mechanics leads to exactly the same experimental predictions as conventional interpretations and it is a fully deterministic theory of particles in motion (not directly measurable), but a motion of a profoundly non-Newtonian sort. From the phase
. Bohm's causal interpretation (today often called the de Broglie-Bohm interpretation) of non-relativistic quantum mechanics leads to exactly the same experimental predictions as conventional interpretations and it is a fully deterministic theory of particles in motion (not directly measurable), but a motion of a profoundly non-Newtonian sort. From the phase 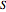 of the wavefunction in the eikonal form
of the wavefunction in the eikonal form 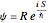 , the velocity in the configuration space is found by
, the velocity in the configuration space is found by 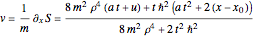 , with
, with
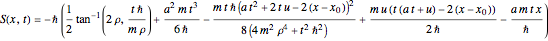 .
.
Integrating  with respect to time the analytic result for
with respect to time the analytic result for 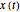 is
is 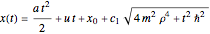 , where
, where 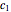 is the integration constant, which is used to estimated the positions of the initial particles. The quantum particle acceleration is
is the integration constant, which is used to estimated the positions of the initial particles. The quantum particle acceleration is 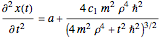 , which is compared with the classical particle acceleration
, which is compared with the classical particle acceleration 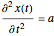 . Considering both cases, three differences are obvious: First, the quantum motion is a superposition of classical terms (with
. Considering both cases, three differences are obvious: First, the quantum motion is a superposition of classical terms (with  , the group velocity) and a term due to the spreading of the packet, which is not affected by the external field. Second, the quantum motion in the uniform field does depend on the mass. Third, increasing the mass
, the group velocity) and a term due to the spreading of the packet, which is not affected by the external field. Second, the quantum motion in the uniform field does depend on the mass. Third, increasing the mass 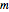 leads to the classical acceleration
leads to the classical acceleration  (from an observation by Sofia Wechsler). When the particle lies initially at the center of the squared wavefunction (
(from an observation by Sofia Wechsler). When the particle lies initially at the center of the squared wavefunction ( ) the motion becomes classical. In the causal interpretation, the effective potential is the sum of quantum potential
) the motion becomes classical. In the causal interpretation, the effective potential is the sum of quantum potential 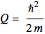
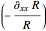 and potential
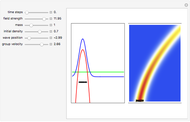
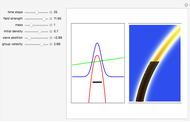
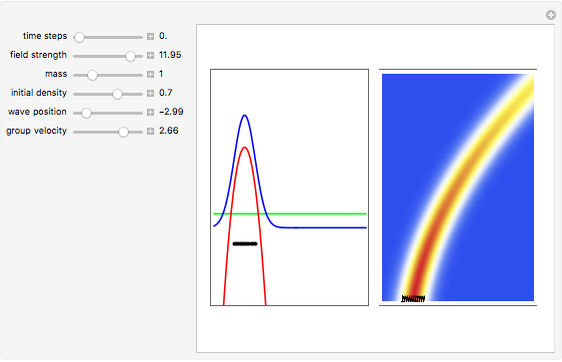
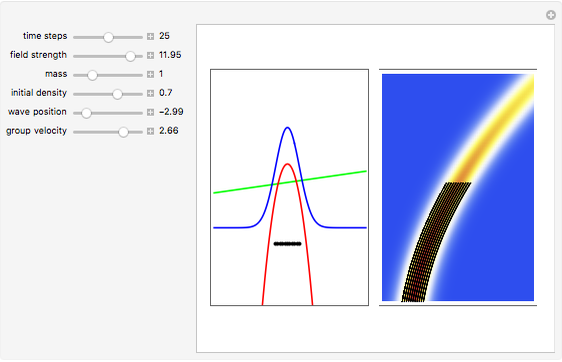
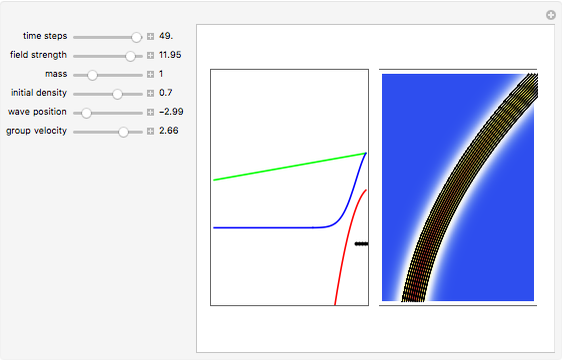
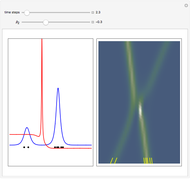
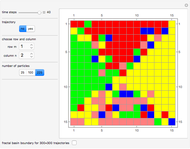
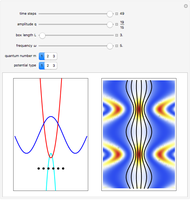
and potential 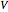 . On the right side, the graphic shows the squared wavefunction and the trajectories. On the left side, you can see the position of the particles, the squared wavefunction (blue), the quantum potential (red), and the velocity (green). The velocity is scaled down.
. On the right side, the graphic shows the squared wavefunction and the trajectories. On the left side, you can see the position of the particles, the squared wavefunction (blue), the quantum potential (red), and the velocity (green). The velocity is scaled down.
[less]
Details
Reference
[1] P. Holland, The Quantum Theory of Motion, Cambridge: Cambridge University Press, 1993.

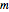 in a uniform gravitational potential
in a uniform gravitational potential 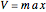 (in the Earth's gravitational field:
(in the Earth's gravitational field: 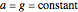 ). The equations of motion can be solved analytically for the classical and quantum-mechanical case. For the classical (i.e., Newtonian) case, the force is
). The equations of motion can be solved analytically for the classical and quantum-mechanical case. For the classical (i.e., Newtonian) case, the force is 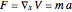 , which leads to the kinematic equation of motion:
, which leads to the kinematic equation of motion: 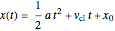 with constant acceleration
with constant acceleration  , constant initial velocity
, constant initial velocity 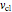 , and initial position
, and initial position 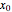 . Classically, the kinematic equation is independent of the mass, which shows that all bodies with different masses fall with an equal acceleration
. Classically, the kinematic equation is independent of the mass, which shows that all bodies with different masses fall with an equal acceleration  . In the quantum case the time-evolution of the wavefunction for an initial Gaussian packet (initial maximum
. In the quantum case the time-evolution of the wavefunction for an initial Gaussian packet (initial maximum 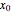 , group velocity
, group velocity  , initial density
, initial density  , mass
, mass 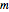 ) in a uniform field with the strength
) in a uniform field with the strength  is described by a complex-valued field:
is described by a complex-valued field: