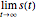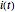Herd Immunity for Smallpox

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
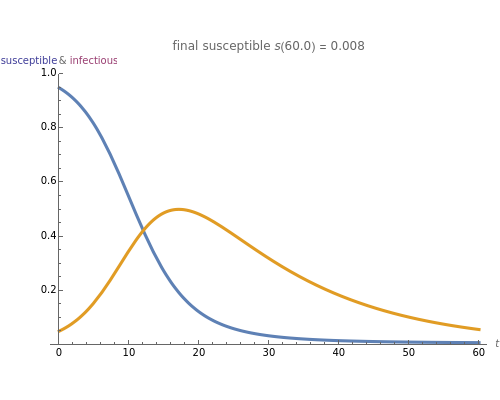
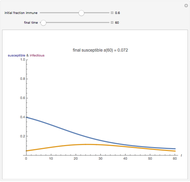
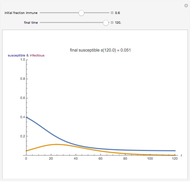
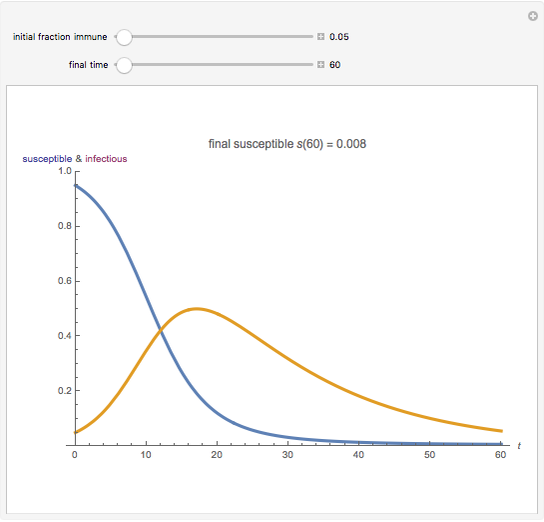
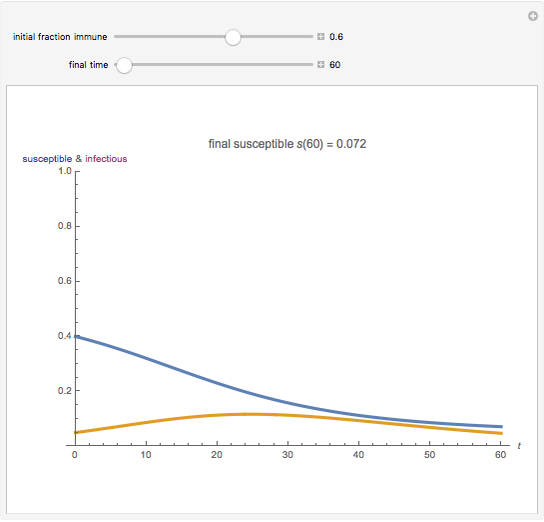
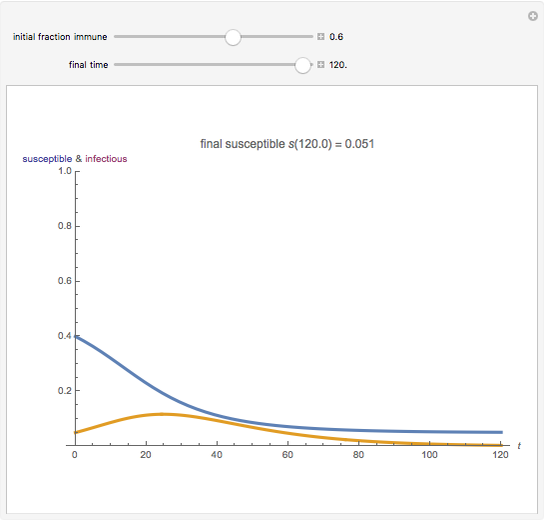
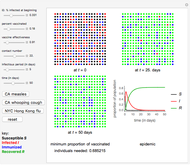
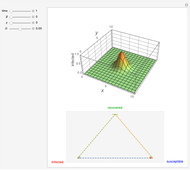
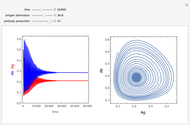
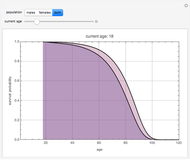
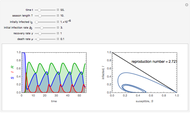
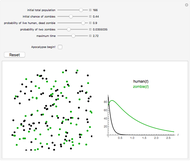
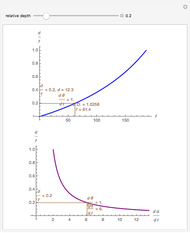
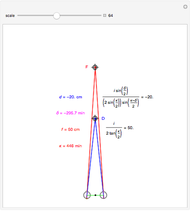
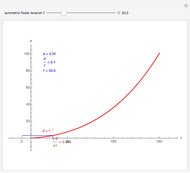
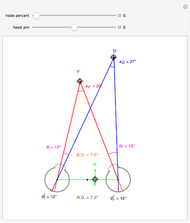
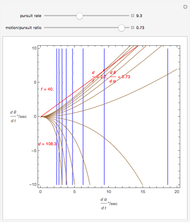
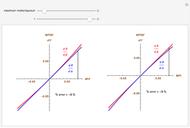
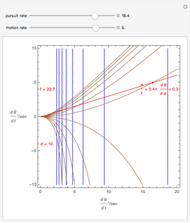
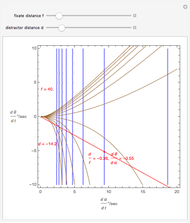
A population has "herd immunity" when the immune population is high enough so that if an infection is introduced, it dies out without building up. You can see this by sliding the initial immune fraction until the red graph does not increase in the illustration for smallpox.
[more]
Contributed by: Keith Stroyan (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation
"Herd Immunity for Smallpox"
http://demonstrations.wolfram.com/HerdImmunityForSmallpox/
Wolfram Demonstrations Project
Published: March 7 2011