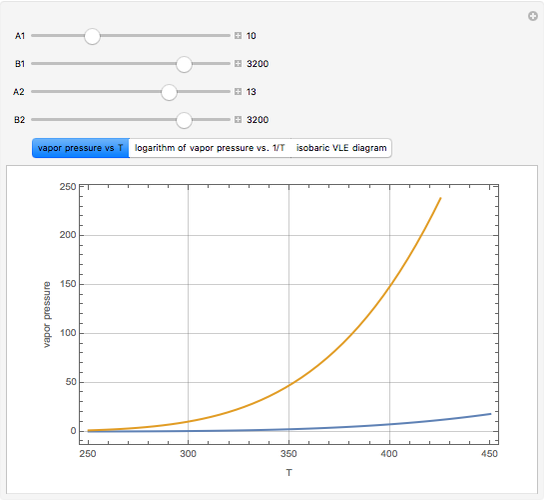
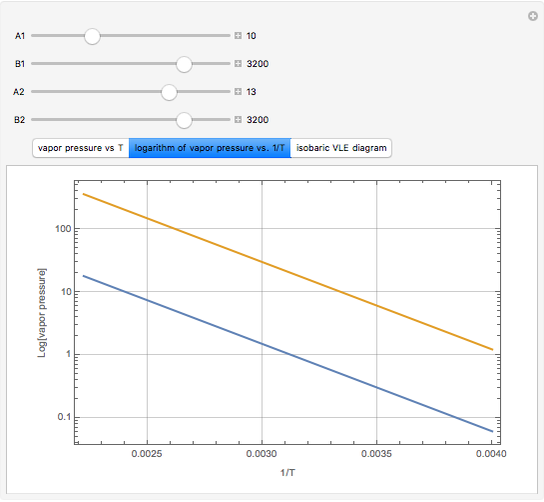
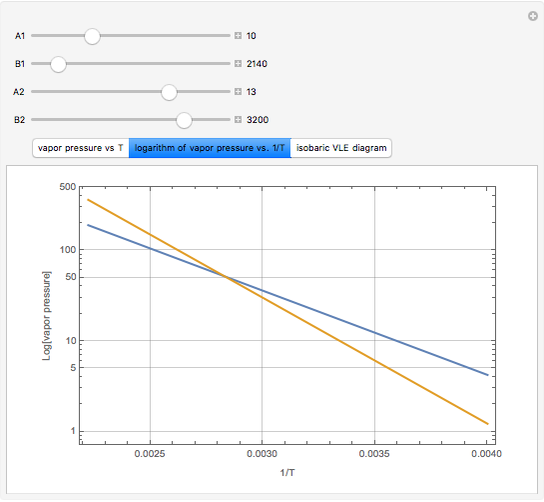
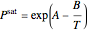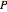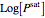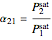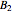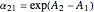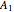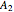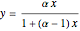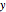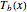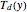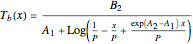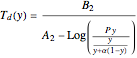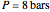One of the simplest equations relating vapor pressure of a pure component to temperature is given by:
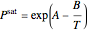 where
where  is in Kelvin and
is in Kelvin and 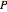 is in bars.
is in bars.
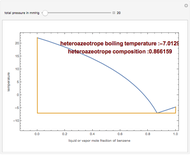
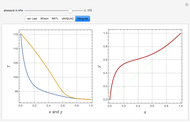
The above equation is named August equation, after the German physicist Ernst Ferdinand August (1795-1870). Thus, 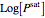 vs.
vs.  is a straight line. As shown in the snapshots, if
is a straight line. As shown in the snapshots, if  , then the two straight lines (i.e., vapor pressures for two components,
, then the two straight lines (i.e., vapor pressures for two components,  and
and  ) will be parallel.
) will be parallel.
Relative volatility assuming ideal behavior is given by: 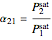 . If the constants
. If the constants  and
and 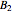 are equal then the relative volatility is independent of temperature and we have
are equal then the relative volatility is independent of temperature and we have 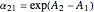 where
where 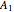 ,
, 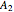 ,
,  and
and 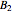 are the constants that appear in the August equation for components
are the constants that appear in the August equation for components  and
and  .
.
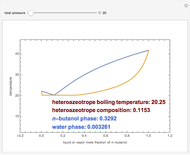
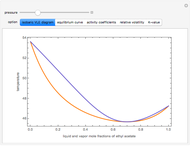
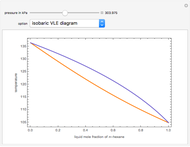
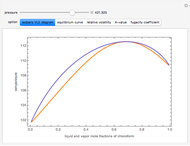
Vapor-liquid equilibrium data can be easily computed for constant relative volatility binary mixtures. Indeed, the following relationships can be derived:
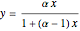
where 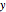 and
and  are the mole fraction of the vapor and liquid phases in equilibrium.
are the mole fraction of the vapor and liquid phases in equilibrium.
One also has analytical expressions for the bubble temperature, 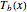 ,and for the dew temperature,
,and for the dew temperature, 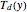 , which are as follows:
, which are as follows:
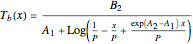
and 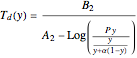
where 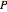 is the total pressure,
is the total pressure, 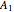 ,
, 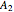 ,
,  and
and 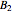 are the constants that appear in the August equation for components
are the constants that appear in the August equation for components  and
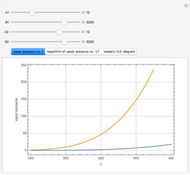
and  and α is the relative volatility. One snapshot shows the isobaric vapor-liquid equilibrium diagram for a particular constant relative volatility mixture at
and α is the relative volatility. One snapshot shows the isobaric vapor-liquid equilibrium diagram for a particular constant relative volatility mixture at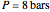 .
.
[less]