The Russian Option: Reduced Regret

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
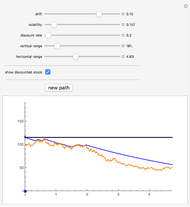
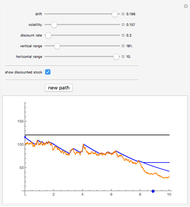
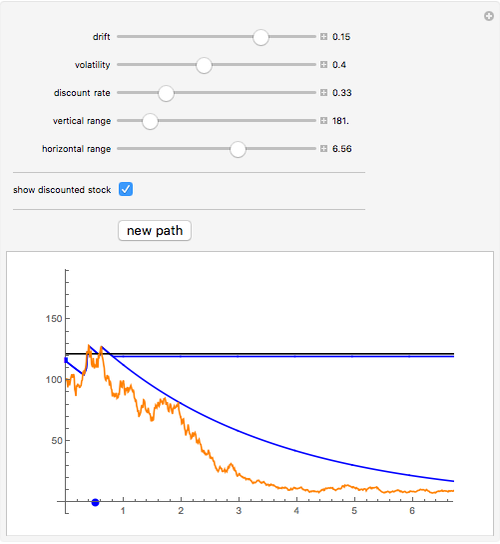
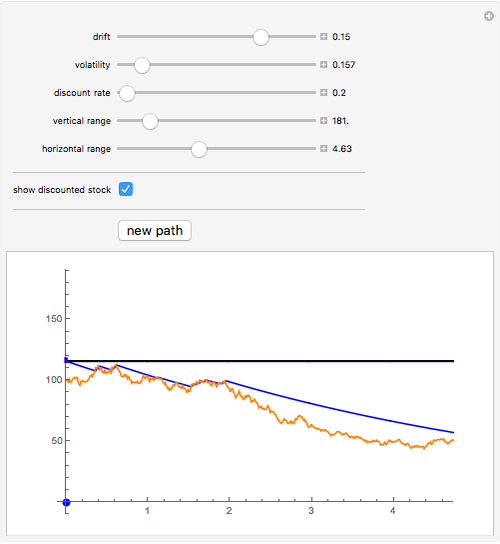
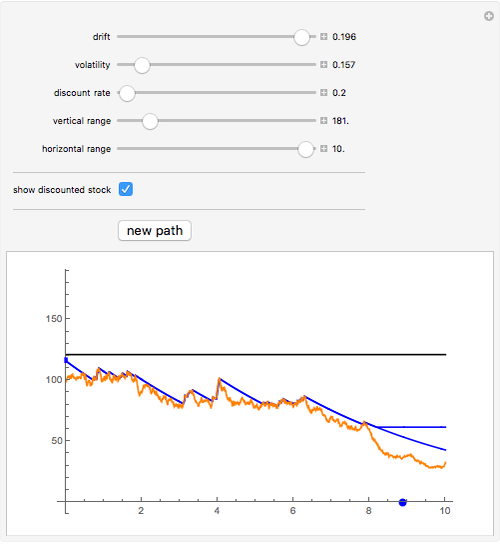
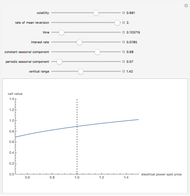
A Russian option is a perpetual American-type option that pays the owner upon exercise the historical maximum price of the stock (this is supposed to "reduce the regret" of not exercising the option at the right time). The option was invented by L. Shepp and A. N. Shirayev and named "the Russian option". Although it is not traded in practice, several remarkable formulas for the option value, optimal exercise time, and the expected exercise time (under the assumption that the stock follows the Black–Scholes model) have been found and have had an important impact on probability theory.
[more]
Contributed by: Andrzej Kozlowski (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Shepp and Shiryayev defined the Russian option in pure mathematical terms. Consider a share whose price  follows a geometric Brownian motion with drift
follows a geometric Brownian motion with drift  and volatility
and volatility  (they also consider the case where the share price follows a Brownian motion with drift—i.e., the Bachelier model). Let
(they also consider the case where the share price follows a Brownian motion with drift—i.e., the Bachelier model). Let 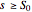 and let
and let 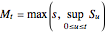 be the payoff of the option at time
be the payoff of the option at time 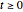 . The task is to maximize the expected value of the discounted payoff
. The task is to maximize the expected value of the discounted payoff  over all stopping times
over all stopping times  . In financial terms the problem can be expressed as follows. The owner of a Russian option chooses an exercise date, represented by a stopping time
. In financial terms the problem can be expressed as follows. The owner of a Russian option chooses an exercise date, represented by a stopping time  , and then receives either
, and then receives either  or the maximum stock price achieved up to this exercise time, whichever is larger, discounted by
or the maximum stock price achieved up to this exercise time, whichever is larger, discounted by 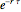 . Shepp and Shiryaev showed that there is a number
. Shepp and Shiryaev showed that there is a number  that depends only on
that depends only on  ,
,  , and
, and  , such that the optimal strategy is to exercise the option at the first time
, such that the optimal strategy is to exercise the option at the first time  such that
such that 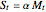 (and the payoff is
(and the payoff is 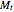 ). This they define as the fair value of the option. It is crucial that
). This they define as the fair value of the option. It is crucial that  is larger than
is larger than  , otherwise it is never optimal to exercise the option. In terms of arbitrage theory one can assume that the stock pays a continuous dividend
, otherwise it is never optimal to exercise the option. In terms of arbitrage theory one can assume that the stock pays a continuous dividend 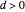 and take
and take  . In this case, the Shepp and Shirayev "fair price" is also the "arbitrage price" of the option.
. In this case, the Shepp and Shirayev "fair price" is also the "arbitrage price" of the option.
The original proof of Shepp and Shirayev was based basically on "guessing" the correct formula for the option price by being guided by Kolmogorov's principle of smooth fit (which they say was a part of the reason for the name of the option) and then proving that the conjectured answer was the right one. Subsequently several other proofs have been given, for example in [2], in which a formula for the expected waiting time for optimal exercise is also given. This value is represented by the blue dot on the (horizontal) time axis.
In [3] the problem of valuing a finite horizon Russian option was solved. As in the case of standard American options there are no explicit formulas and the option value is given as the solution of a nonlinear integral equation that has to be solved by numerical methods.
[1] L. Shepp and A. N. Shiryaev, "The Russian Option:Reduced Regret," The Annals of Applied Probability, 3, 1993 pp. 631–640.
[2] S. E. Graverseb and G. Peskir, "On the Russian Option: The Expected Waiting Time," Theory Probab. Appl., 42(3), 1997 pp. 564–575.
[3] G. Peskir, "The Russian Option: Finite Horizon," Finance Stochast., 9, 2005 pp. 251–267.
Permanent Citation
"The Russian Option: Reduced Regret"
http://demonstrations.wolfram.com/TheRussianOptionReducedRegret/
Wolfram Demonstrations Project
Published: March 7 2011