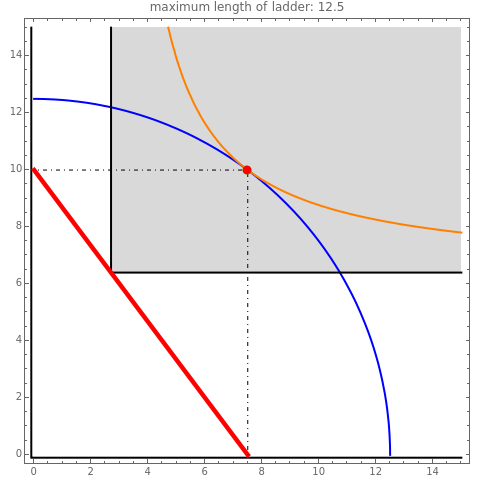
The Ladder around the Corner Problem
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
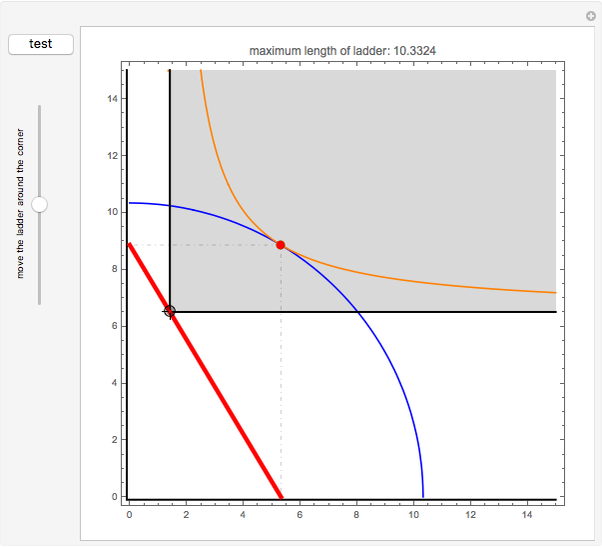
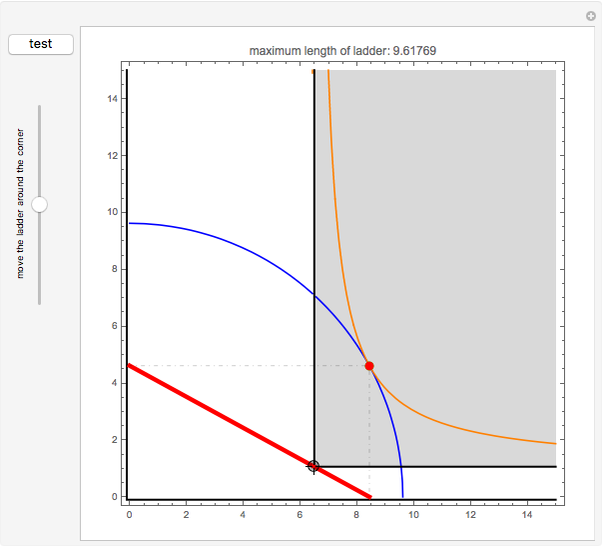
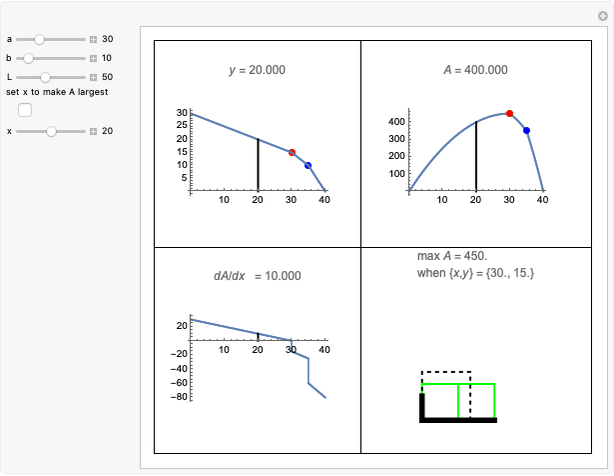
This Demonstration visualizes a typical problem of constrained optimization: find the maximum length of a ladder that can be moved horizontally around the corner between two perpendicular corridors of different widths  and
and  .
.
Contributed by: Erik Mahieu (December 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] C. Rao, "The Ladder around a Corner Room," Chaitanya's Random Pages (blog). (Nov 7, 2010) ckrao.wordpress.com/2010/11/07/the-ladder-around-a-corner-problem.
Permanent Citation