Hedging the European Put Option

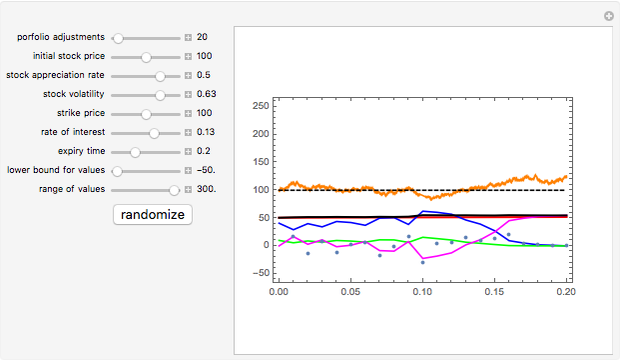
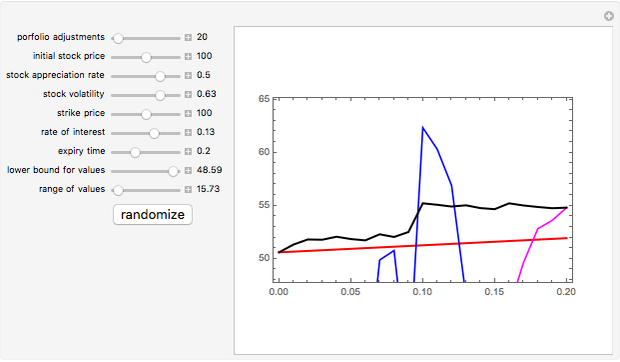
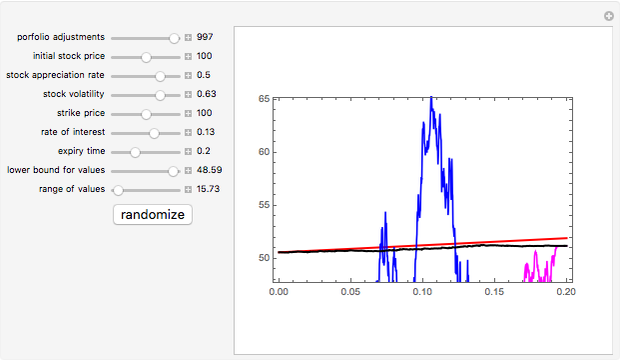
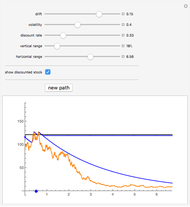
This Demonstration illustrates the so-called delta-hedging argument that is used to derive the Black–Scholes formula for the price of a European put option on stock in the Black–Scholes model. The sample path of a stock price following an exponential Brownian process is shown colored orange (mouse over a curve to display its description). The strike price is represented by the dashed black line. A portfolio is constructed consisting of one put option on the stock, an amount of stock (equal to -Δ, where Δ is the derivative of the Black–Scholes price of the option with respect to the stock price), and a money market account. The portfolio is adjusted at regular intervals (you choose the number of times) and the proceeds from the transactions (shown as points in the graph) are invested in the money market. The total value of the portfolio, which is the sum of the value of the option (green line), value of the stock held (blue line), and the money market account (magenta line) is almost deterministic. Zooming in on this brokerage account line (by using the two bottom sliders) reveals the presence of randomness, which can be eliminated by increasing the number of portfolio adjustments.