A Noncontinuous Limit of a Sequence of Continuous Functions
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
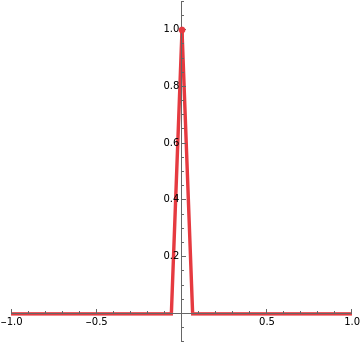
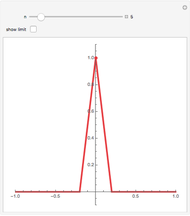
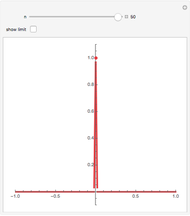
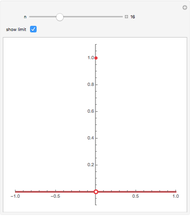
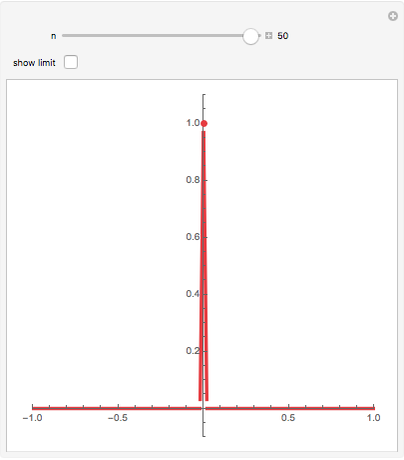
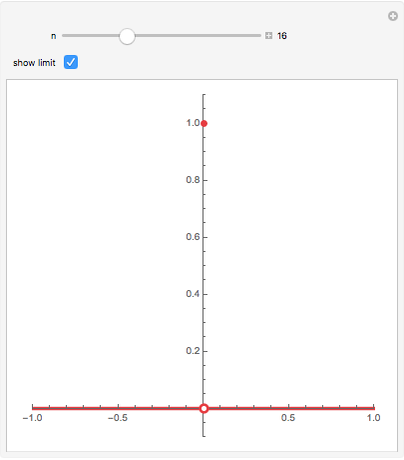
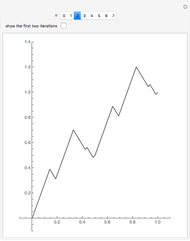
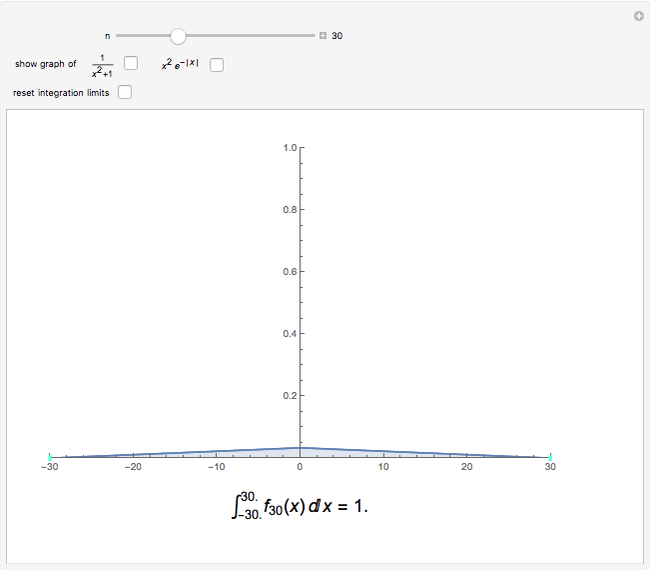
Consider a sequence  of continuous real-valued functions of a real variable. The sequence
of continuous real-valued functions of a real variable. The sequence  converges pointwise on a set
converges pointwise on a set 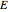 to a function
to a function  if for each
if for each  in
in 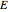 ,
,  as
as 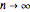 . The limit
. The limit  is not guaranteed to be continuous; in this Demonstration the limit has a removable discontinuity. (To construct a limit that is discontinuous everywhere in
is not guaranteed to be continuous; in this Demonstration the limit has a removable discontinuity. (To construct a limit that is discontinuous everywhere in 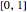 , construct
, construct  with spikes at all numbers that can be written in the form
with spikes at all numbers that can be written in the form 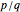 , where
, where  and
and  are positive integers and
are positive integers and 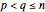 .)
.)
Contributed by: George Beck (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation