Transformation of Icosahedral Solids in Z15

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
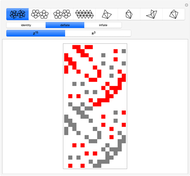
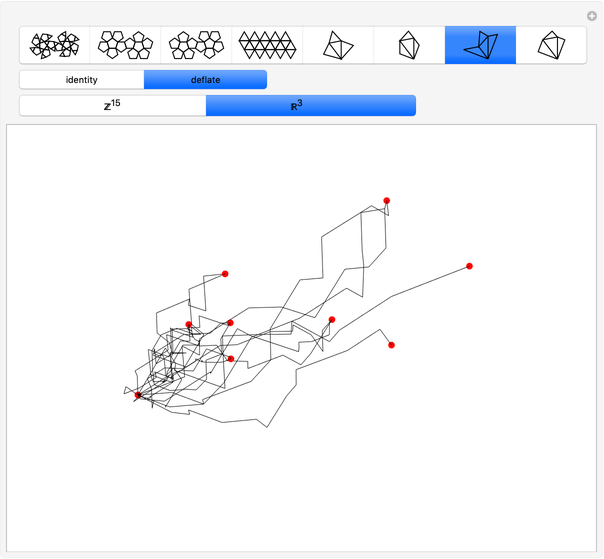
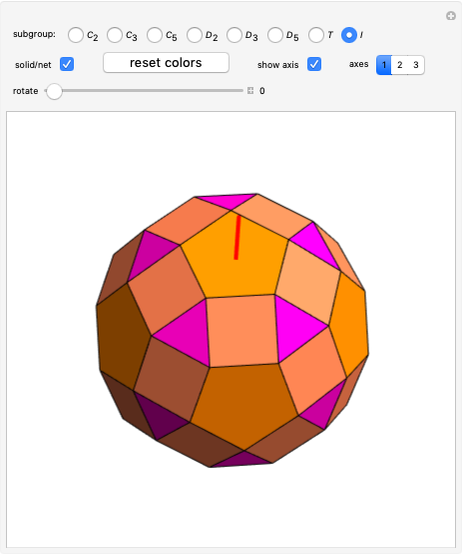
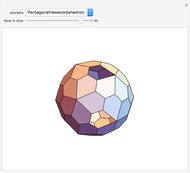
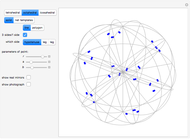
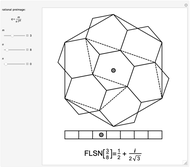
This Demonstration relates the deflation of the space-filling Danzer tetrahedra, "A", "B", "C", and "K", to the transformation of three solids with full icosahedral symmetry: an icosidodecahedron, two equivalent dodecahedra, and an icosahedron. All transformations are computed in 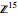 and projected into Euclidean space. Transformations that move points away from the origin are depicted as paths of connected line segments. For each transformation, the display shows only one element of the entire set of paths, which contains a number of elements equal to the factorial of the rank of the transformation.
and projected into Euclidean space. Transformations that move points away from the origin are depicted as paths of connected line segments. For each transformation, the display shows only one element of the entire set of paths, which contains a number of elements equal to the factorial of the rank of the transformation.
Contributed by: Brad Klee (July 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Mathematical models of icosahedral quasicrystals created using replacement rules relate to the golden ratio in many ways. The distance between any two vertices of a tiling can always be expressed in 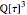 . Also, each iteration of the replacement rules increases the volume of the tiling by a factor of
. Also, each iteration of the replacement rules increases the volume of the tiling by a factor of  , necessitating that each linear dimension increases by a factor of
, necessitating that each linear dimension increases by a factor of  .
.
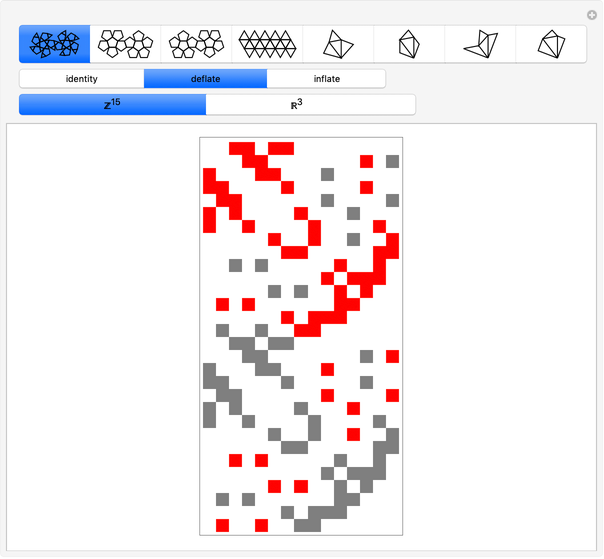
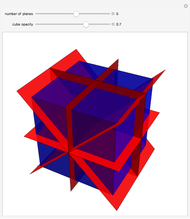
In a 15-dimensional space of integers 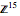 (
( , from zählen, to count), the representation of the icosidodecahedron is very simple: a positive identity matrix joined to a negative identity matrix. A projection of this shape into
, from zählen, to count), the representation of the icosidodecahedron is very simple: a positive identity matrix joined to a negative identity matrix. A projection of this shape into 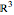 takes the dot product of the 30×15 matrix representation with a 15×3 matrix containing half of the icosidodecahedron's coordinates expressed in
takes the dot product of the 30×15 matrix representation with a 15×3 matrix containing half of the icosidodecahedron's coordinates expressed in 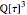 . Sums of these coordinates can generate the coordinates of two equivalent dodecahedra and the coordinates of an icosahedron. Without multiplying by any irrational number, the coordinates of an icosidodecahedron can also sum together to generate the coordinates of another icosidodecahedron scaled by a factor of twice the golden ratio or scaled by a factor of twice the inverse of the golden ratio. The existence of inflation and deflation summations for each of these three solids with full icosahedral symmetry creates a set of transformations relating any point in
. Sums of these coordinates can generate the coordinates of two equivalent dodecahedra and the coordinates of an icosahedron. Without multiplying by any irrational number, the coordinates of an icosidodecahedron can also sum together to generate the coordinates of another icosidodecahedron scaled by a factor of twice the golden ratio or scaled by a factor of twice the inverse of the golden ratio. The existence of inflation and deflation summations for each of these three solids with full icosahedral symmetry creates a set of transformations relating any point in 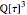 to at least one point in a 15-dimensional, integer-only space,
to at least one point in a 15-dimensional, integer-only space, 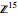 .
.
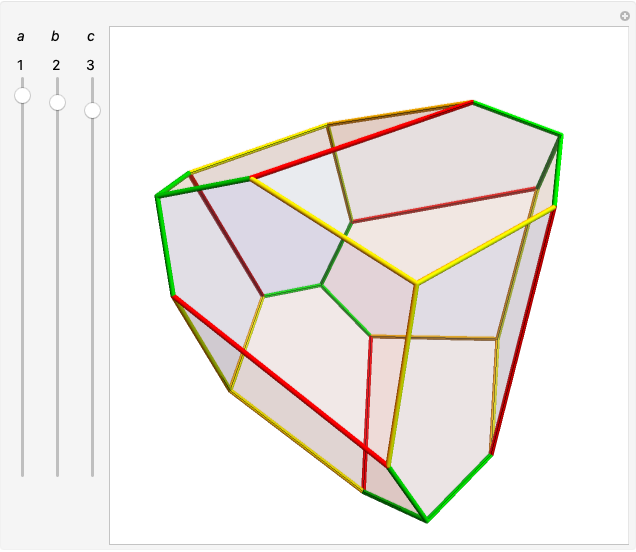
The coordinates for the space-filling tetrahedra derived by Ludwig Danzer and other members of Dortmund's Q-team are always incident on an axis of icosahedral symmetry when the origin is a particular vertex of the tetrahedra, as are the vertices for the icosahedron, dodecahedron, and icosidodecahedron when the origin is the average of all coordinates. As the replacement rules copy the tetrahedra throughout space, scaling, translation, and rotation do not change the field of the coordinates away from 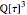 . Therefore, a vector separating any two vertices of the Danzer tiling can be written as a sum of 15 vectors, each with its own integer coefficient.
. Therefore, a vector separating any two vertices of the Danzer tiling can be written as a sum of 15 vectors, each with its own integer coefficient.
References
[1] E. O. Harriss, "On Canonical Substitution Tilings," PhD thesis, Imperial College London, 2004.
[2] L. Danzer, P. Sonneborn, G. van Ophuysen, and S. Duitmann, The {A, B, C, K} Book, Dortmund: University of Dortmund, 1993.
More complete source code can be downloaded from Irreducible Aperiodic Bases @ GitHub.
Permanent Citation