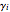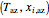Azeotropes of Binary Mixtures Containing Ethanol

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
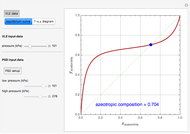
When a liquid mixture boils at a given temperature 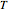 and pressure
and pressure 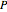 , the composition of vapor
, the composition of vapor  is typically different from the liquid composition
is typically different from the liquid composition  ., but this is not always the case. With some mixtures it is possible to have a boiling condition
., but this is not always the case. With some mixtures it is possible to have a boiling condition  such that the composition of the vapor leaving is the same as the composition of the boiling liquid:
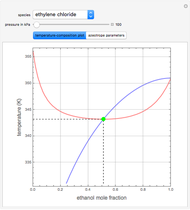
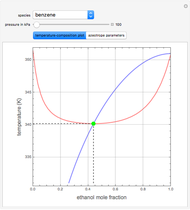
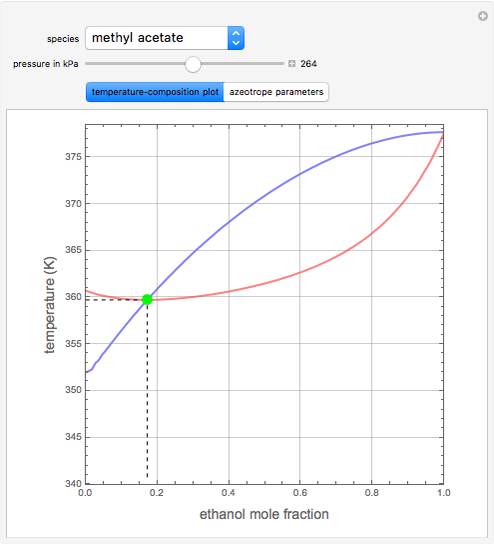
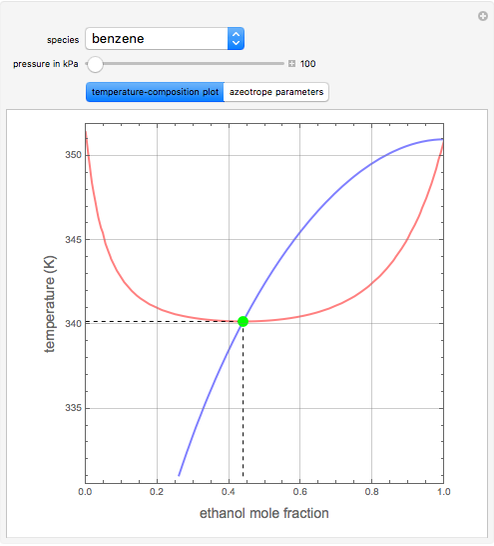
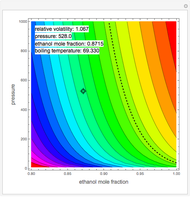
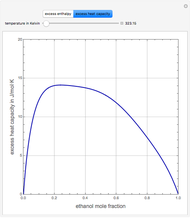
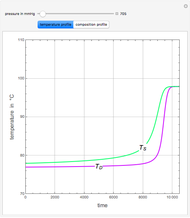
such that the composition of the vapor leaving is the same as the composition of the boiling liquid:  . This boiling mixture is called an azeotrope. Azeotropes (also called constant-boiling mixtures) are classified as either minimum boiling (positive) azeotropes or maximum boiling (negative) azeotropes. In this Demonstration, the azeotropes of binary mixtures containing ethanol are computed. You can select the second species for the binary mixture from the pull-down menu and use a slider to specify the system pressure
. This boiling mixture is called an azeotrope. Azeotropes (also called constant-boiling mixtures) are classified as either minimum boiling (positive) azeotropes or maximum boiling (negative) azeotropes. In this Demonstration, the azeotropes of binary mixtures containing ethanol are computed. You can select the second species for the binary mixture from the pull-down menu and use a slider to specify the system pressure 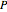 . All the azeotropes computed for the ethanol mixtures are minimum boiling azeotropes.
. All the azeotropes computed for the ethanol mixtures are minimum boiling azeotropes.
Contributed by: Housam Binousand Brian G. Higgins (April 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
S. I. Sandler, Chemical, Biochemical and Engineering Thermodynamics, 4th ed., New Work: John Wiley & Sons, 2006.
Permanent Citation