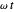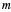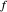Electromagnetic Waves in Optical Fibers

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
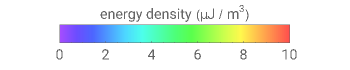
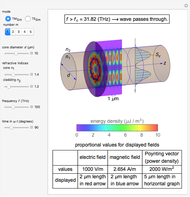
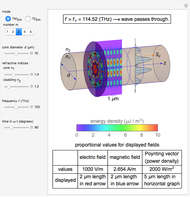
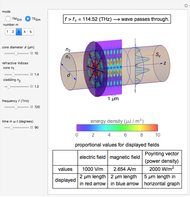
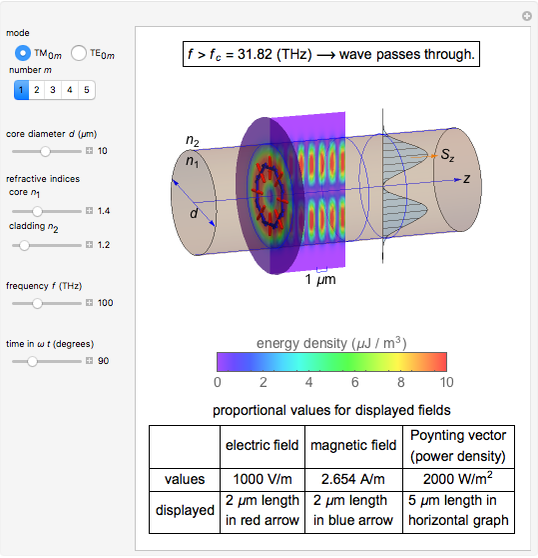
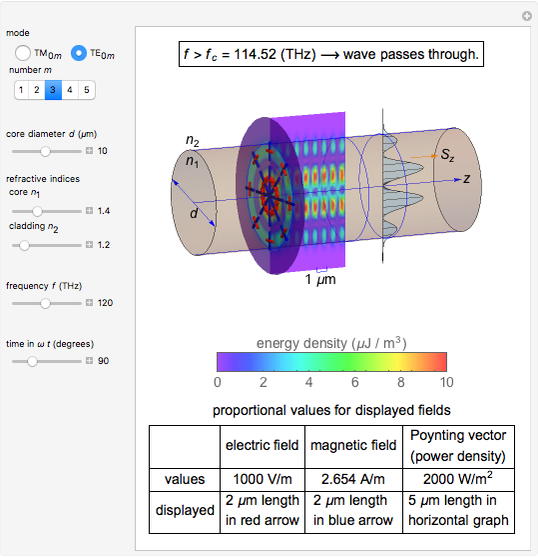
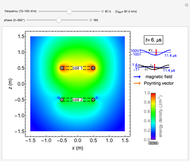
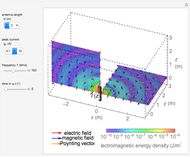
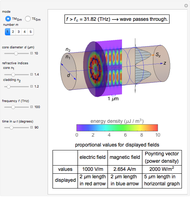
Light or other electromagnetic waves can propagate through optical fibers. This Demonstration visualizes the field, energy distribution, and propagation of light in step index fibers. A step index fiber is composed of a core and cladding that have different refractive indices
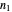 and
and 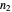
 , respectively. Many modes are possible, including the transverse magnetic (TM) and transverse electric (TE) waves, of which the zeroth modes
, respectively. Many modes are possible, including the transverse magnetic (TM) and transverse electric (TE) waves, of which the zeroth modes 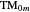 and
and 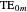 are chosen here.
are chosen here.
Contributed by: Y. Shibuya (December 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshot 1: fields for 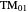 mode for a fiber of 10
mode for a fiber of 10  m diameter at
m diameter at 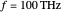
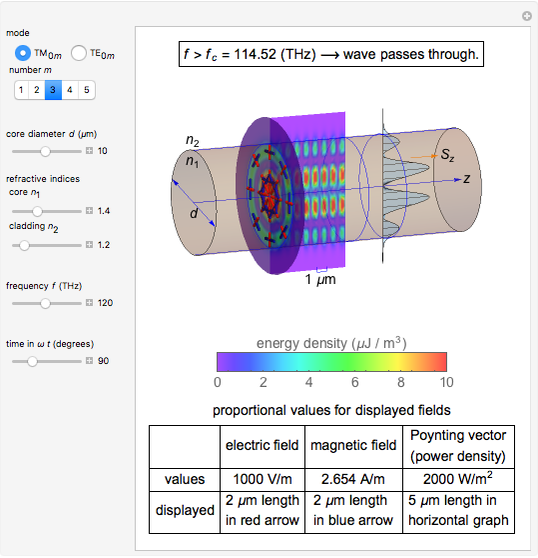
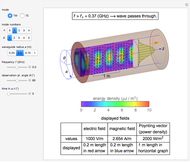
Snapshot 2: fields of 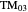 mode for a fiber of 10
mode for a fiber of 10  m diameter at
m diameter at 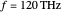
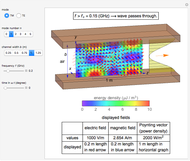
Snapshot 3: fields of 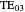 mode for a fiber of 10
mode for a fiber of 10  m diameter at
m diameter at 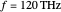
The periodic solution of the wave equation for the modes 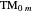 and
and 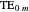 has to be axisymmetrical. In the case of
has to be axisymmetrical. In the case of 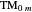 , for example, it takes the form
, for example, it takes the form
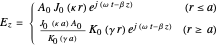 .
.
Here 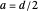 is the core radius and
is the core radius and 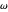 is the angular frequency. Considering the connection conditions for other field components leads to transcendental equations:
is the angular frequency. Considering the connection conditions for other field components leads to transcendental equations:
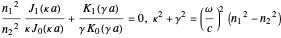 .
.
The values of  and
and 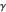 are the
are the 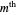 roots of the characteristic equations. There is a cut-off frequency
roots of the characteristic equations. There is a cut-off frequency 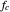 determined by the fiber property and the value
determined by the fiber property and the value 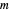 . The frequency has to be higher than
. The frequency has to be higher than 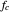 in order for there to be a solution for
in order for there to be a solution for  and
and 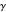 . The cut-off frequency is the same for the TM and TE modes, but the values of
. The cut-off frequency is the same for the TM and TE modes, but the values of  and
and 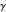 are different because of a slight difference in the characteristic equations. Once
are different because of a slight difference in the characteristic equations. Once  and
and 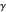 are determined,
are determined, 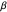 is obtained from the relation
is obtained from the relation 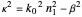
 The constant
The constant 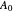 is set so that the maximum electric field is 1000 V/m. Other field components can then be readily calculated.
is set so that the maximum electric field is 1000 V/m. Other field components can then be readily calculated.
For the sake of simplicity, the electrical and magnetic fields are shown in the areas where the power flow is at a maximum. The energy density is calculated by 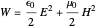 , where
, where 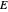 and
and 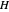 are the instantaneous field values. The average Poynting vector is given by
are the instantaneous field values. The average Poynting vector is given by 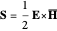 , for which the
, for which the  component is evaluated and shown in the graph. The cladding takes a fraction of the power in the vicinity of core.
component is evaluated and shown in the graph. The cladding takes a fraction of the power in the vicinity of core.
The step index fibers are known as a multi-mode fibers. More modes are possible beside the simple TM and EM modes shown here.
Reference
[1] T. Okoshi, et al., Optical Fibers (in Japanese), Tokyo: Ohm Publishing Co., 1983.
Permanent Citation