Hydrogenic Radial Functions via Supersymmetry

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
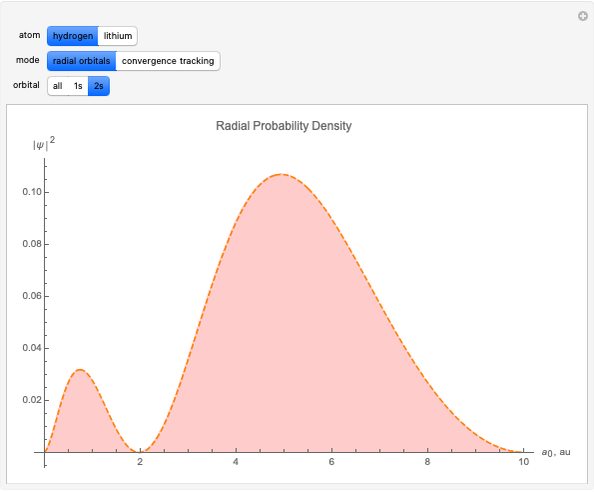
An application of supersymmetric quantum mechanics enables all the bound-state radial functions for the hydrogen atom to be evaluated using first-order differential operators, without any explicit reference to Laguerre polynomials.
[more]
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Supersymmetric quantum mechanics can be applied to the solution of the hydrogenic radial equation, treated as a pseudo-one-dimensional problem in the variable  with effective Hamiltonians denoted
with effective Hamiltonians denoted  . There exist two partner Hamiltonians for each value of
. There exist two partner Hamiltonians for each value of  , which can be written
, which can be written  and
and  , with
, with  and
and  . The superpotential
. The superpotential  is given by
is given by  . With
. With  as defined above,
as defined above, 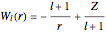 . The lowest-energy eigenstate of
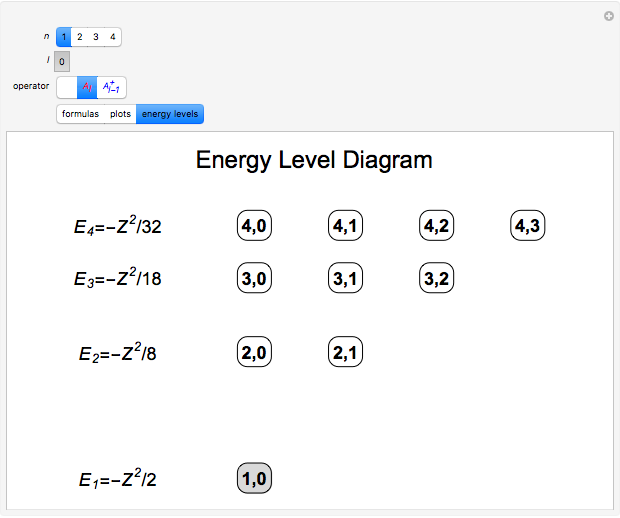
. The lowest-energy eigenstate of  has no partner eigenstate, but all higher-energy eigenstates have degenerate supersymmetric partners. These can be labeled by increasing values of the principal quantum number
has no partner eigenstate, but all higher-energy eigenstates have degenerate supersymmetric partners. These can be labeled by increasing values of the principal quantum number  , beginning with
, beginning with  . The composite pattern for all
. The composite pattern for all  -values leads to the characteristic degeneracies for
-values leads to the characteristic degeneracies for  in a pure Coulomb field, associated with a higher symmetry than would be implied by spherical invariance alone.
in a pure Coulomb field, associated with a higher symmetry than would be implied by spherical invariance alone.
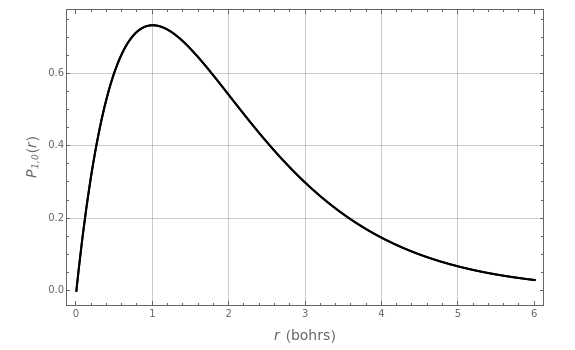
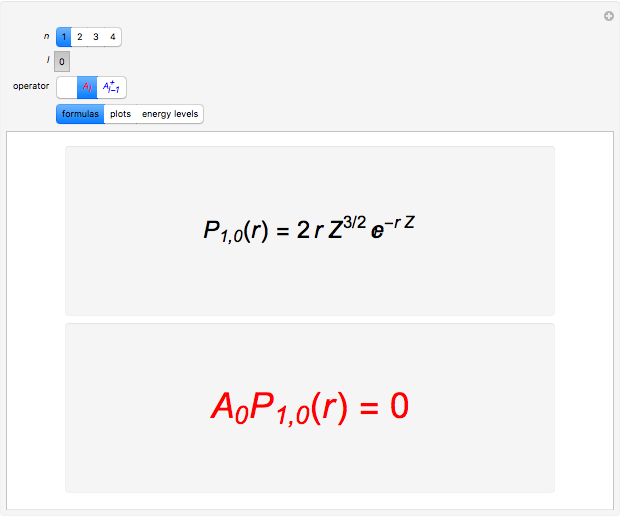
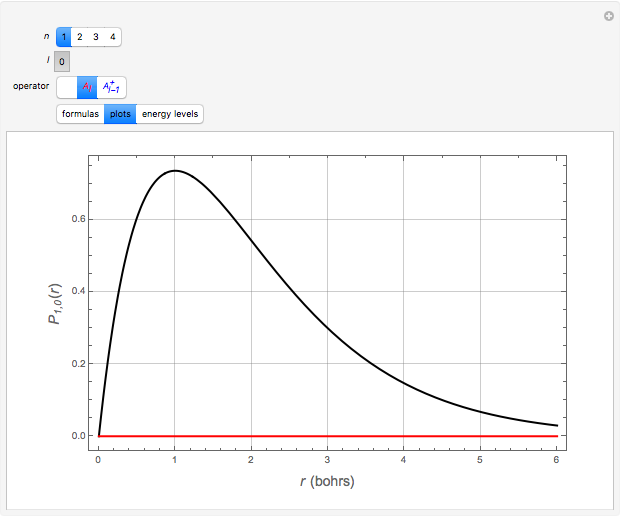
Snapshots 1–3: the 1 ground state is nondegenerate and is annihilated by either operator
ground state is nondegenerate and is annihilated by either operator  or
or 
Snapshots 4–6: the 3 state is transformed to 3
state is transformed to 3 by
by 
Reference: A. Valance, T. J. Morgan, and H. Bergeron, "Eigensolution of the Coulomb Hamiltonian via Supersymmetry," American Journal of Physics, 58(5), 1990 pp. 487–491.
Permanent Citation