Leontief Production Function

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
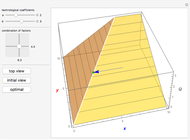
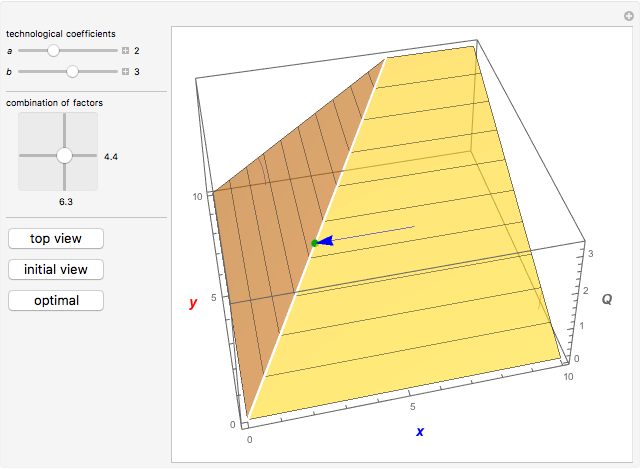
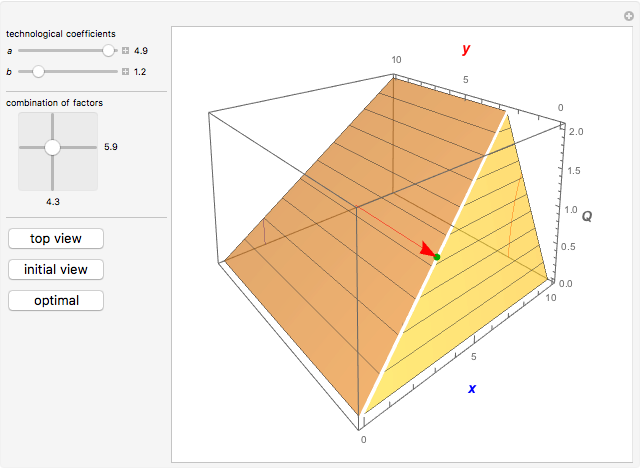
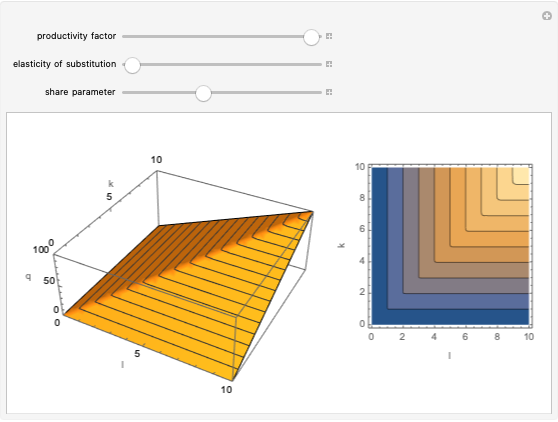
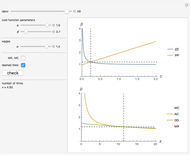
This Demonstration studies the Leontief production function of the form  in three dimensions. The main feature of the function is that it models the situation when production factors
in three dimensions. The main feature of the function is that it models the situation when production factors  and
and  are perfect complements to each other.
are perfect complements to each other.
Contributed by: Timur Gareev (May 2018)
Open content licensed under CC BY-NC-SA
Snapshots
Details
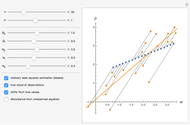
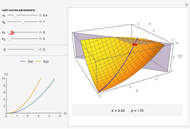
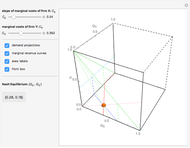
A Leontief production function of the form

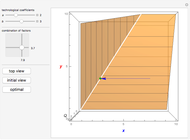
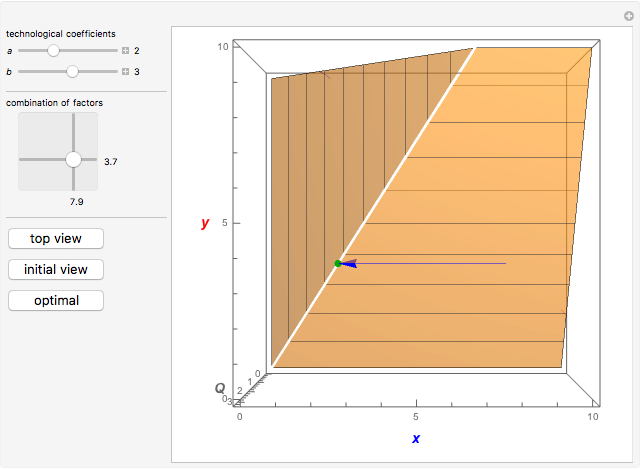
has all its optimal solutions lying on the line
 .
.
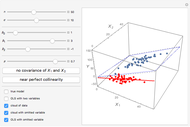
Factors  and
and  are perfect complements in the model. To shift from one optimal solution to another, a producer has to change both factors in the established proportion
are perfect complements in the model. To shift from one optimal solution to another, a producer has to change both factors in the established proportion  . If we take an arbitrary point
. If we take an arbitrary point  lying outside the optimal direction, a redundancy (inefficiency) exists. On the three-dimensional plot, the size of the inefficiency corresponds to the length of the blue or red arrow. The blue arrow shows how much of resource
lying outside the optimal direction, a redundancy (inefficiency) exists. On the three-dimensional plot, the size of the inefficiency corresponds to the length of the blue or red arrow. The blue arrow shows how much of resource  can be saved without reducing
can be saved without reducing  . The red arrow shows the same thing for
. The red arrow shows the same thing for  .
.
The Leontief function has no partial derivatives in kink points lying on the optimal direction  . Nonetheless, it has directional derivatives in points along the vector
. Nonetheless, it has directional derivatives in points along the vector  , which are equal to
, which are equal to  .
.
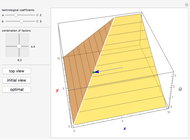
We also show blue and red angles with tangents  and
and  , respectively. The angles show that the model is the result of the intersection of two planes
, respectively. The angles show that the model is the result of the intersection of two planes  and
and  , and changes to
, and changes to  or
or  move their respective planes.
move their respective planes.
Use the "top view" button to see a classical two-dimensional representation of the model.
Note also that in the context of consumer theory, the same model can be interpreted as a utility function.
Permanent Citation