Omitted Variable Bias in 3D

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
This Demonstration develops geometric intuition behind the concept of omitted variable bias. In econometrics modeling, there is a persistent risk of omitting an important variable (i.e. due to not understanding the true model structure or due to a lack of relevant data). As a result, endogeneity [1] spoils the model, resulting in inconsistent and therefore misleading estimations of model coefficients. Usually the effect of the omitted variable is explained analytically or via numerical examples, but visualization may bring more insight to the issue.
[more]
Contributed by: Timur Gareev (May 2018)
Open content licensed under CC BY-NC-SA
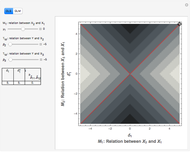
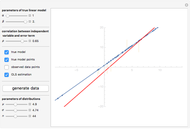
Snapshots
Details
If we try to estimate a true model of the form

with an incorrect model of the form
 ,
,
the estimation of  , which is signed
, which is signed  , is most likely biased. Indeed, we have by definition:
, is most likely biased. Indeed, we have by definition:
 .
.
Here we have
 ;
;

and
 .
.
The element  is an error term vector, where each observation term is independent (from each other) and normally distributed with mean 0 and variance
is an error term vector, where each observation term is independent (from each other) and normally distributed with mean 0 and variance  .
.
The key term in the preceding expression is  , which we can simulate with the
, which we can simulate with the  control. If it equals zero, no problems arise—estimations are unbiased,
control. If it equals zero, no problems arise—estimations are unbiased,  . However, in practice the important feature of the model of the form
. However, in practice the important feature of the model of the form

is that  , and so omitting
, and so omitting  from the evaluation causes bias. It is always a source of confusion, but
from the evaluation causes bias. It is always a source of confusion, but  should not be too high, otherwise results even without omitted variables will be misleading (as we approach the other "trap" in the form of multicollinearity).
should not be too high, otherwise results even without omitted variables will be misleading (as we approach the other "trap" in the form of multicollinearity).
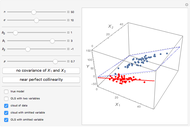
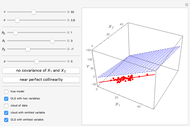
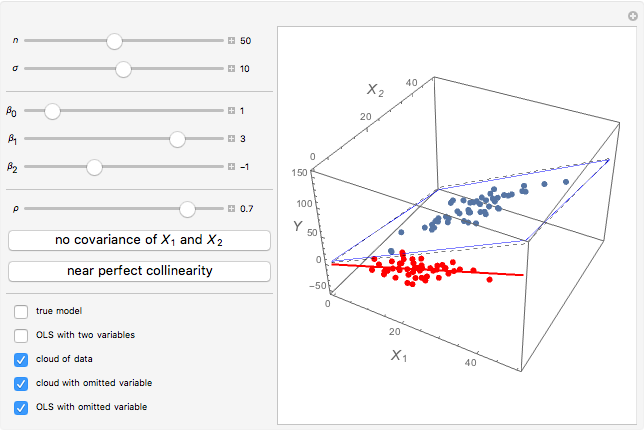
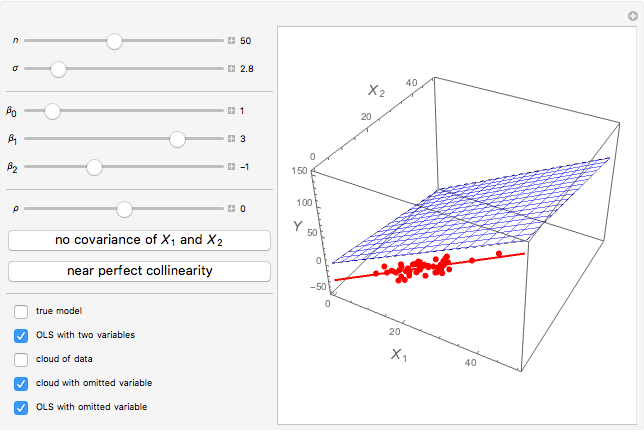
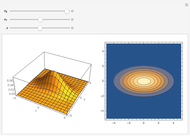
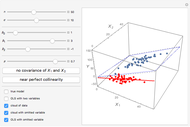
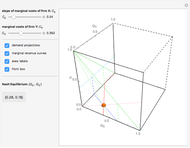
We demonstrate it as follows. The blue cloud is the observations cloud, and each point stands for one observation (the number of observations may be changed with  ). The black lattice shows the true model. The blue lattice reflects the correct estimation with both variables
). The black lattice shows the true model. The blue lattice reflects the correct estimation with both variables  and
and  included. The red line is the regression with the omitted variable. (The red cloud is the projection of the observations cloud from true 3D space to 2D.) Use the checkboxes to switch the appearance of elements on and off. When you use the checkboxes, the cloud does not change. Be warned, though, that each time parameters change, the cloud of observation changes as well.
included. The red line is the regression with the omitted variable. (The red cloud is the projection of the observations cloud from true 3D space to 2D.) Use the checkboxes to switch the appearance of elements on and off. When you use the checkboxes, the cloud does not change. Be warned, though, that each time parameters change, the cloud of observation changes as well.
Most important are the slopes of black and blue planes and the red line. When the slopes are relatively equal, there is no bias.
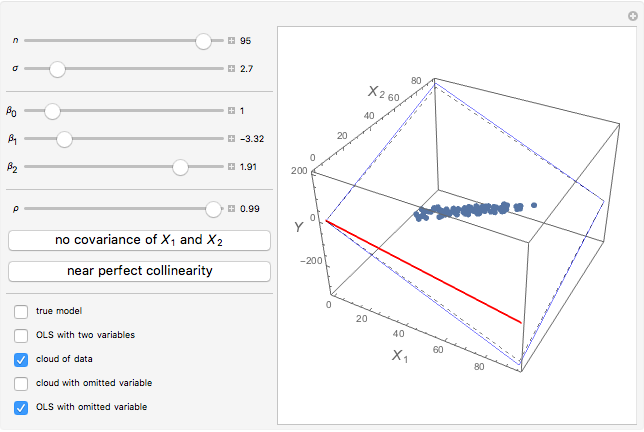
Increasing  and reducing
and reducing  may considerably reduce bias. Use the buttons to study special cases with
may considerably reduce bias. Use the buttons to study special cases with  or
or  (
( corresponds to perfect multicollinearity, so we cannot study this case). It is also recommended to check
corresponds to perfect multicollinearity, so we cannot study this case). It is also recommended to check  visually.
visually.
Reference
[1] Wikipedia. "Endogeneity (Econometrics)." (May 7, 2018) en.wikipedia.org/wiki/Endogeneity_(econometrics).
Permanent Citation