Best Response in Static Two-Player Games

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
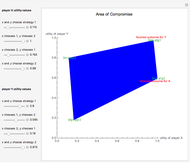
This Demonstration gives a visual interpretation of the best response in static two-player games using an example from a textbook on game theory [1, pp. 59]. The game is considered from the viewpoint of the first player, as it is easier to visualize strategies if an opponent is limited to just two strategies.
Contributed by: Timur Gareev (June 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
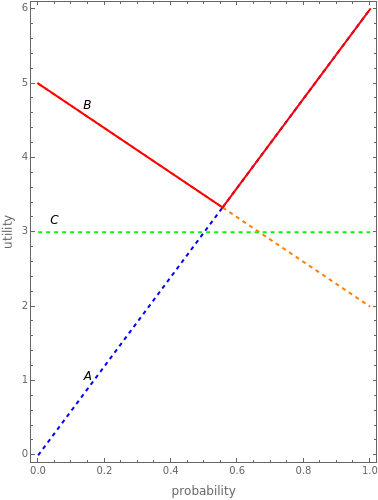
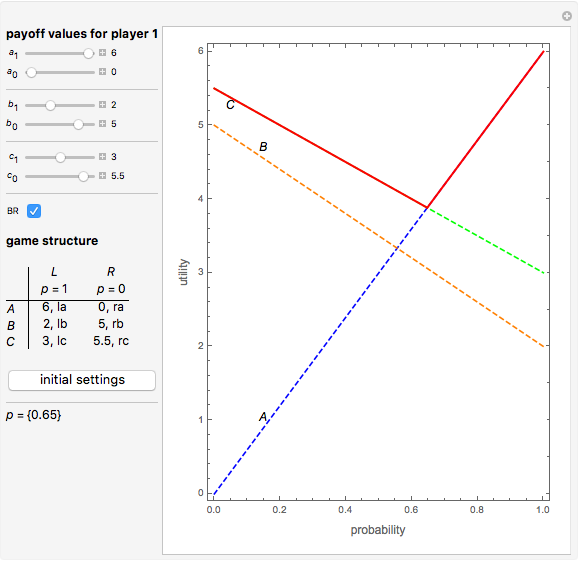
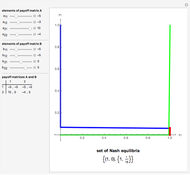
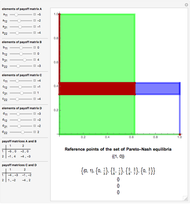
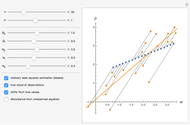
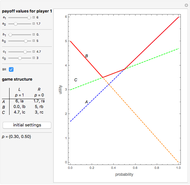
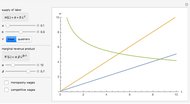
The game structure panel gives a two-player game with payoff matrix. For simplicity, only the first player's utilities are shown, leaving the second player's parameters as placeholders; they do not play a decisive role in the analysis. The first player's strategies are the set  , and the second player's strategies are
, and the second player's strategies are  .
.
The best response is determined by the beliefs of a player, which is a distribution of probabilities over the strategies of the other player [1, pp. 39].
If player 1 believes that player 2 will choose strategy  with probability
with probability  , then her best response will be determined by the red line. If
, then her best response will be determined by the red line. If  , then the second player may play only pure strategies,
, then the second player may play only pure strategies,  or
or  . The fact that
. The fact that  gets any value within the interval
gets any value within the interval  reflects uncertainty of the first player about the behavior of the opponent.
reflects uncertainty of the first player about the behavior of the opponent.
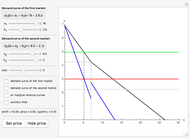
In theory, player 1 should be guided only by personal beliefs in order to make a rational decision. Look closely at the best response function (thick red line). This is, in essence, the function that maps beliefs to strategies. Consider an example when  lies between the values 0 and 1 with the initial setting
lies between the values 0 and 1 with the initial setting  . This means that if
. This means that if  , then player 1 activates strategy
, then player 1 activates strategy  ; if
; if 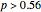 , then strategy
, then strategy  obviously brings a larger payoff. Finally, at the vertex, the player may choose
obviously brings a larger payoff. Finally, at the vertex, the player may choose  or
or  . With the initial setting, there is no provision for the rational playing of strategy
. With the initial setting, there is no provision for the rational playing of strategy  .
.
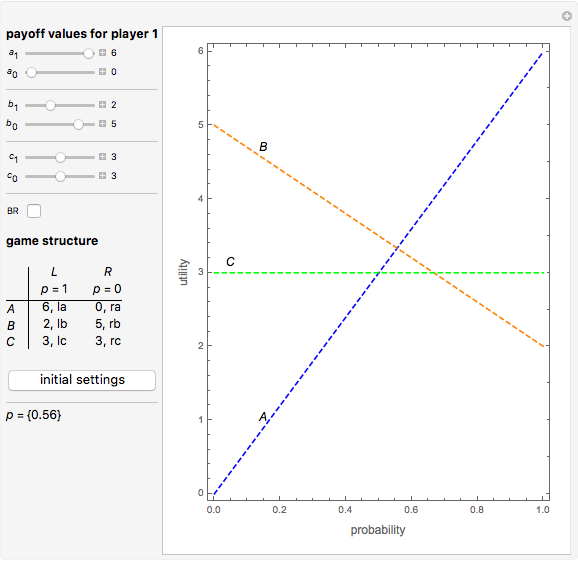
The best response is closely related to the concept of dominance. To consider an example, click the "initial settings" button. You can see that strategy  is never a best response, which means it is strictly dominated by the combination of the other strategies,
is never a best response, which means it is strictly dominated by the combination of the other strategies,  and
and  . When you vary the sliders, the payoff matrix is changed for the first player, and so the game changes.
. When you vary the sliders, the payoff matrix is changed for the first player, and so the game changes.
It is important to understand that a player forms a response taking into account her own beliefs concerning probabilities of the strategies of the opponent. Player payoffs determine the form of the best response. Concrete values of the utilities of the opponent, even if known to the player, may affect the beliefs but do not change the model.
Click the "BR" checkbox to see the best response of the first player in the game.
Reference
[1] J. Watson, Strategy: An Introduction to Game Theory, 2nd ed., New York: W. W. Norton, 2008.
Permanent Citation