Endogeneity Bias

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
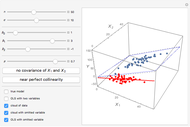
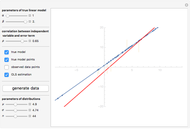
Endogeneity is one of the major concerns of contemporary empirical studies in economics and econometrics. This Demonstration aims to show the geometric sense of this phenomenon in the simplest setting, namely the model with one single explanatory variable (also known as the independent variable).
[more]
Contributed by: Timur Gareev (February 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
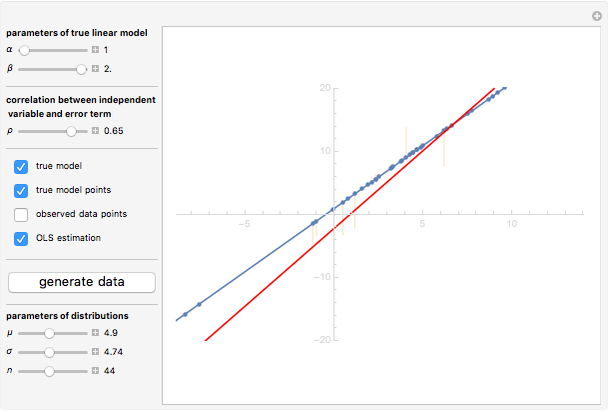
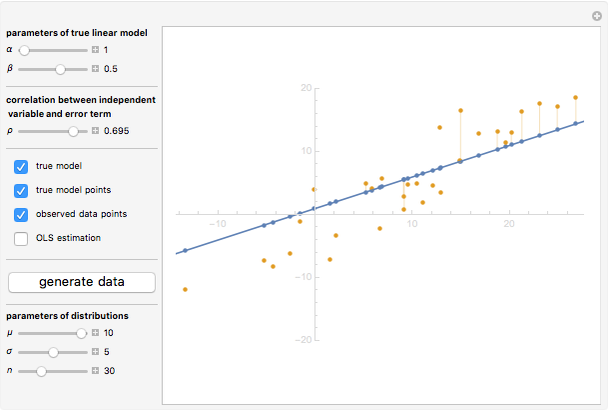
Endogeneity bias (in the narrow sense) is applicable to the model if  . Whenever
. Whenever  (meaning that the independent variable
(meaning that the independent variable  is not correlated with the error term
is not correlated with the error term  ), there is no endogeneity bias (in the narrow sense). In this case, the slope of the fitting curve (OLS regression line) converges to the slope of the true line
), there is no endogeneity bias (in the narrow sense). In this case, the slope of the fitting curve (OLS regression line) converges to the slope of the true line  with the growth of the number of observations
with the growth of the number of observations  , or
, or  .
.
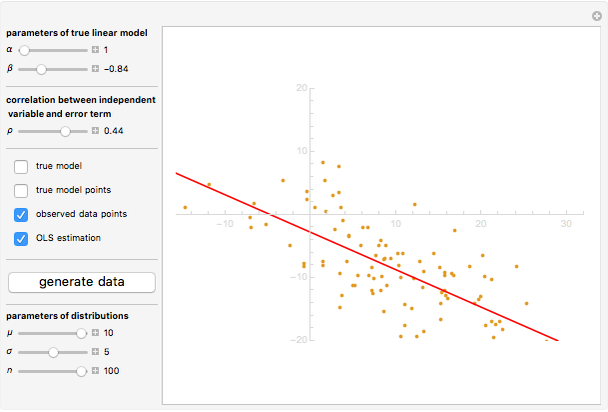
On the contrary, with endogeneity bias there is no such convergence and the fitting model gives inconsistent estimates of  in terms of
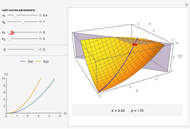
in terms of  . You can also see a geometric representation of endogeneity in that simple case when observations (points on the plot) lie systematically lower or higher than a given true line. That is what makes OLS fitting pointless in the presence of endogeneity bias. There are many reasons of endogeneity, namely, omitted variables, measurement errors, and simultaneity. Methods such as using a control function or instrumental variables (IV) can be applied to cure the endogeneity bias problem.
. You can also see a geometric representation of endogeneity in that simple case when observations (points on the plot) lie systematically lower or higher than a given true line. That is what makes OLS fitting pointless in the presence of endogeneity bias. There are many reasons of endogeneity, namely, omitted variables, measurement errors, and simultaneity. Methods such as using a control function or instrumental variables (IV) can be applied to cure the endogeneity bias problem.
This Demonstration is designed to generate random data by clicking the "generate data" button. You can vary the parameters:  is the number of observations,
is the number of observations,  is both (for simplicity of the model) the expectation and the standard error of the random variate
is both (for simplicity of the model) the expectation and the standard error of the random variate  , and
, and  is the standard error of the normally distributed error term
is the standard error of the normally distributed error term  with
with  expectation.
expectation.
Reference
[1] J. M. Wooldridge, Introductory Econometrics: A Modern Approach, Mason, OH: South-Western, Cengage Learning, 2009 p. 26.
Permanent Citation