Discriminating Monopolist with Two Independent Markets

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
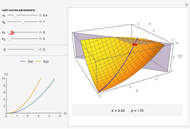
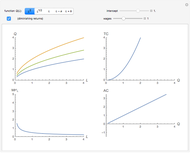
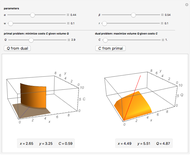
This Demonstration studies an important case in industrial organization: how a discriminating monopolist sets prices in two independent markets. The discriminating monopolist faces a broken curve that we call  , which is a result of "horizontal summation" of the marginal revenue functions of both markets. The monopolist sets prices from the condition
, which is a result of "horizontal summation" of the marginal revenue functions of both markets. The monopolist sets prices from the condition  . This model differs from the important case of nondiscriminating monopoly, with a broken and discontinuous total marginal revenue curve
. This model differs from the important case of nondiscriminating monopoly, with a broken and discontinuous total marginal revenue curve 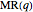 derived from a broken total demand curve. Understanding the difference between
derived from a broken total demand curve. Understanding the difference between  and
and 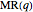 is essential to understanding the models.
is essential to understanding the models.
Contributed by: Timur Gareev (December 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
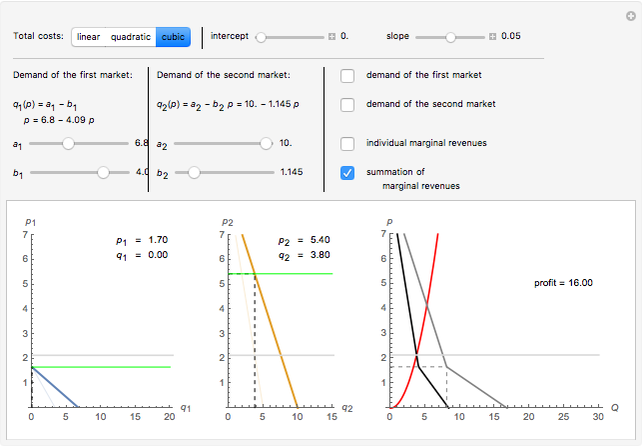
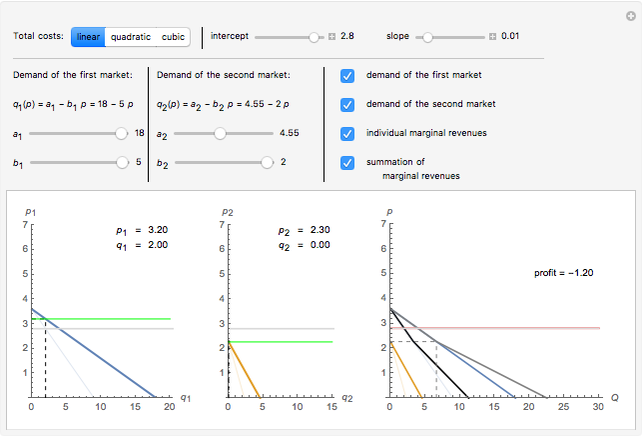
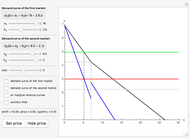
Suppose a monopolist faces two independent markets. In the first market, demand is  , and in the second market, demand is
, and in the second market, demand is  . The monopolist solves the typical problem of setting prices (in conjunction with volume of production) so as to maximize the total profit collected from both markets. We consider the discriminating monopolist, who sets the prices
. The monopolist solves the typical problem of setting prices (in conjunction with volume of production) so as to maximize the total profit collected from both markets. We consider the discriminating monopolist, who sets the prices  and
and  , respectively, for the first and second markets.
, respectively, for the first and second markets.
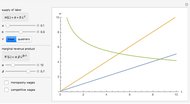
We want to know the total costs  , where
, where  is the total quantity of production. The marginal costs function
is the total quantity of production. The marginal costs function  is the derivative of the total costs function. This means that knowing only the marginal costs is not enough, as we cannot reconstruct the fixed part of the total costs (we have set the fixed costs equal to 2). We find the required optimal price levels from the condition
is the derivative of the total costs function. This means that knowing only the marginal costs is not enough, as we cannot reconstruct the fixed part of the total costs (we have set the fixed costs equal to 2). We find the required optimal price levels from the condition  , where
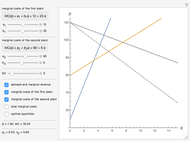
, where  is in fact a result of horizontal summation of individual marginal revenue functions [1, pp. 76–77]. Then we can find the optimal values of
is in fact a result of horizontal summation of individual marginal revenue functions [1, pp. 76–77]. Then we can find the optimal values of  and
and  separately for both markets. Inverse individual demand functions give us the sought-for optimal prices
separately for both markets. Inverse individual demand functions give us the sought-for optimal prices  and
and  followed by the profit calculation:
followed by the profit calculation:  . We model different
. We model different  functions ("linear", "quadratic", and "cubic"), including trivial cases that lead to
functions ("linear", "quadratic", and "cubic"), including trivial cases that lead to  .
.
Note that "slope" and "intercept" sliders control the  curve reflected on the right plot. Use the tooltips on the plots to identify the respective curves. Pay attention to the fact that horizontal summation of different marginal revenues curves
curve reflected on the right plot. Use the tooltips on the plots to identify the respective curves. Pay attention to the fact that horizontal summation of different marginal revenues curves  is not equivalent to the total marginal revenue
is not equivalent to the total marginal revenue  . The monopolist uses this horizontal summation to derive the condition for optimization and then effectively deals with two independent markets with separate marginal revenues. (The case of a nondiscriminating monopolist dealing with total
. The monopolist uses this horizontal summation to derive the condition for optimization and then effectively deals with two independent markets with separate marginal revenues. (The case of a nondiscriminating monopolist dealing with total  is considered in another Demonstration—see the Related Link.)
is considered in another Demonstration—see the Related Link.)
Reference
[1] O. Shy, Industrial Organization: Theory and Applications. Cambrige, MA: MIT Press. 1995.
Permanent Citation