Details

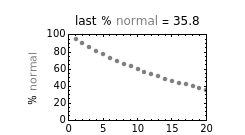
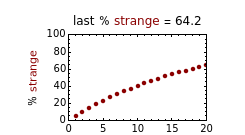
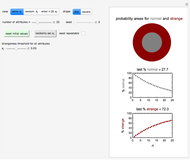
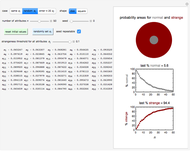
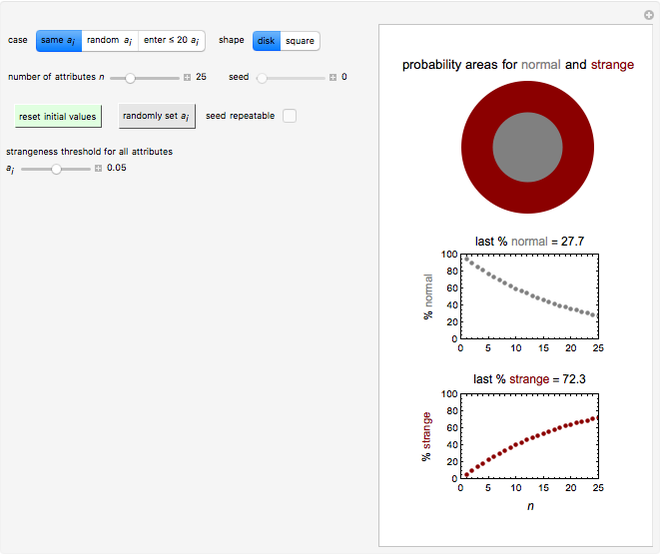
Snapshot 1: normality and strangeness determined by 100 attributes with fixed boundaries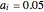

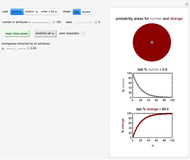
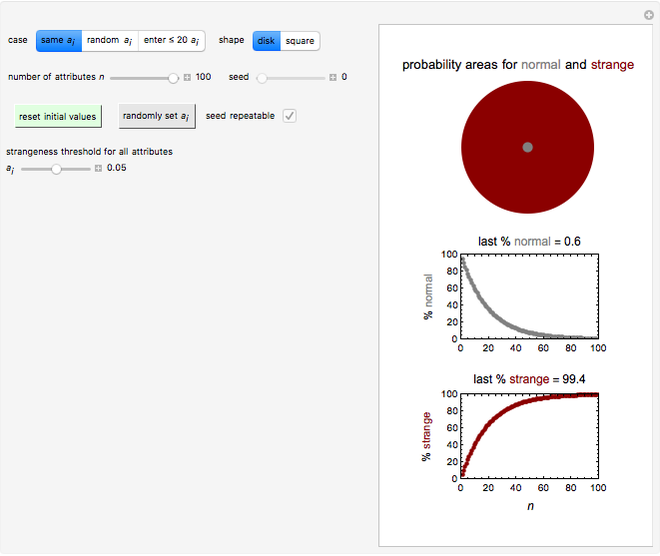
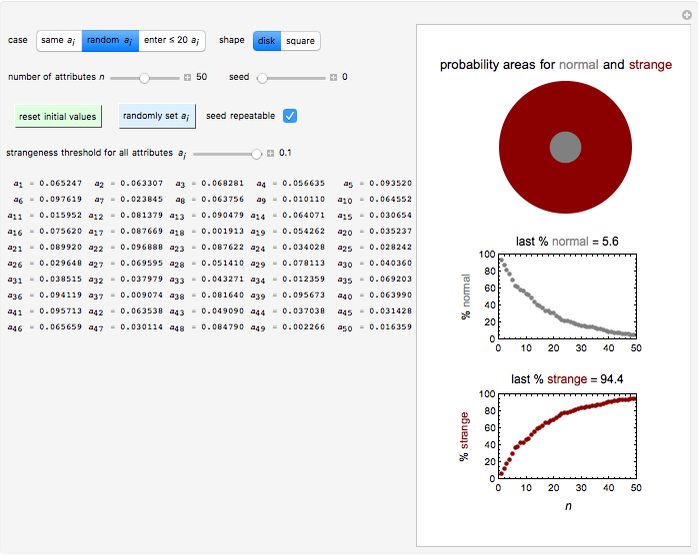
Snapshot 2: normality and strangeness determined by 50 attributes with randomly chosen individual boundaries

Snapshot 3: normality and strangeness determined by 20 attributes with manually chosen individual boundaries

Snapshot 4: normality and strangeness determined by 40 attributes with randomly chosen individual boundaries and showing a square probability area display

According to Paulos [1], strangeness can be defined as being beyond the range considered normal. Assuming for simplicity that a chosen attribute is uniformly distributed, being strange can be defined as being at the top or bottom 5%, for example; then the probability of being normal is 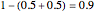or 90% and of being strange is 0.1 or 10%. When a person's normality or strangeness is determined by two attributes, with the same 5% criterion, then the probability of encountering a normal person drops to 0.81 or 81%. For three attributes, it drops to 0.729 or 72.9%; for four attributes it drops to 0.656 or 65.6%; and so on. For 50 attributes, the probability of encountering a normal person drops to 0.515%, and for 100 attributes to only 0.00266%.

Where the strangeness criterion is the same for all the attributes, as in the given example, the probability of encountering a normal person when judged by attributes, that is, by vectors in an -dimensional space, is calculated with the formula 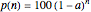, where is the total fraction of the extremes in each of the attributes, 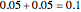as in the given example.

For the more general case where the strangeness criterion is allowed to vary among the attributes (and need not be symmetric), the percent probability of encountering a normal person is calculated by the formula .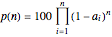

This Demonstration provides visualization of the increasing strangeness and correspondingly diminishing normality in two graphical forms as chosen by the user: (1) a dark red ring whose variable area represents the strangeness probability surrounding a gray disk whose area represents the probability of normality, or (2) a dark red square frame whose variable area represents the strangeness probability surrounding a gray square whose area represents the probability of normality.

This Demonstration plots the increasing probability of strangeness and the diminishing probability of normality as functions of from 1 to a maximum of 100 and displays their (last) numerical values for the chosen in dark red and gray, respectively, above each plot.

The attributes' threshold values can all be the same, determined by the 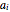slider, if the first setter (case 1: "same 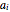") is checked. It can be varied randomly within a chosen range (case 2: "random 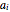"), in which case the number (from 1 to 100) of attributes' actual 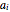values will be displayed. A third option (case 3: "enter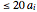") allows for manually entering the 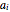values of up to 20 attributes, each with its own slider.

For case 2, each time the blue "randomly set 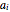" setter is clicked, a new random set of 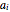values is generated. If the "seed repeatable" box is checked, the same set of random values for all attributes is generated from the value set by the "seed" slider. The initial default settings of all controls may be restored by clicking the green "reset initial values" button.

Notice that this Demonstration only provides a visualization of the general concept using the simplest uniform distribution function, without making any attempt to identify actual attributes and their thresholds.

Reference

[1] J. A. Paulos, A Numerate Life: A Mathematician Explores the Vagaries of Life, His Own and Probably Yours, Amherst, NY: Prometheus Books, 2015.