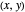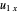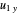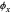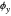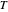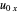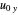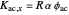Motion of Single Ion in a Linear Paul Trap

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
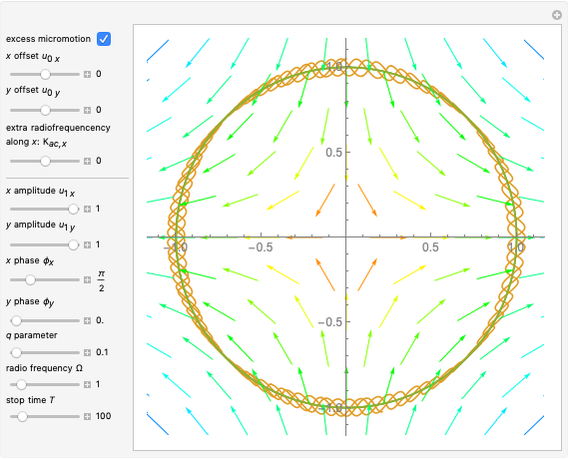
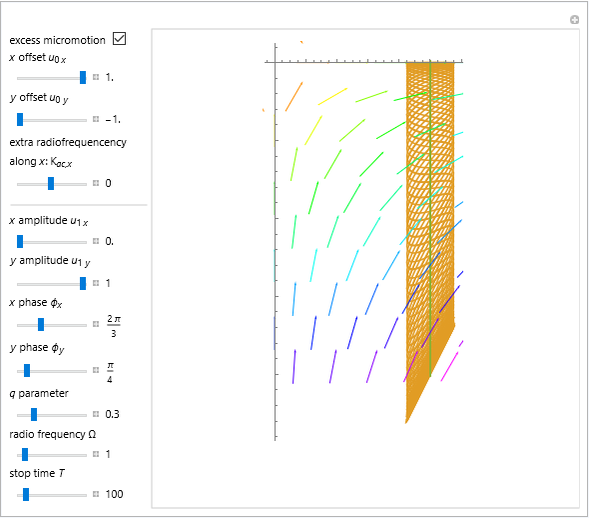
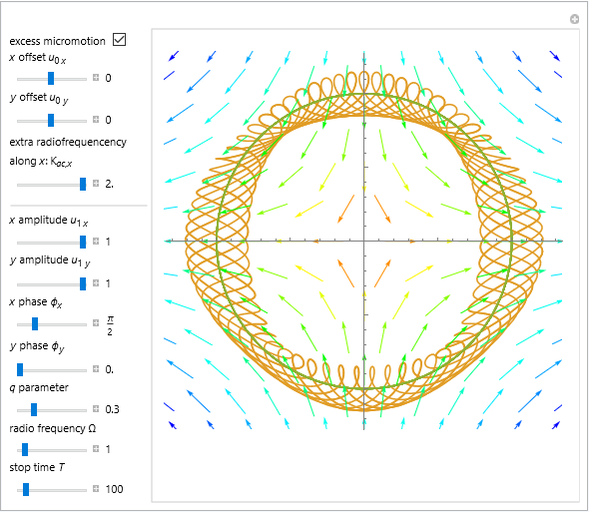
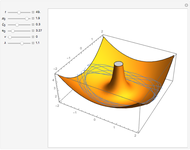
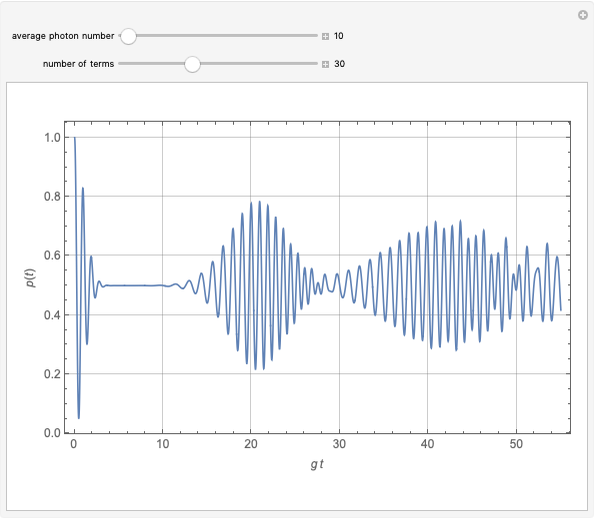
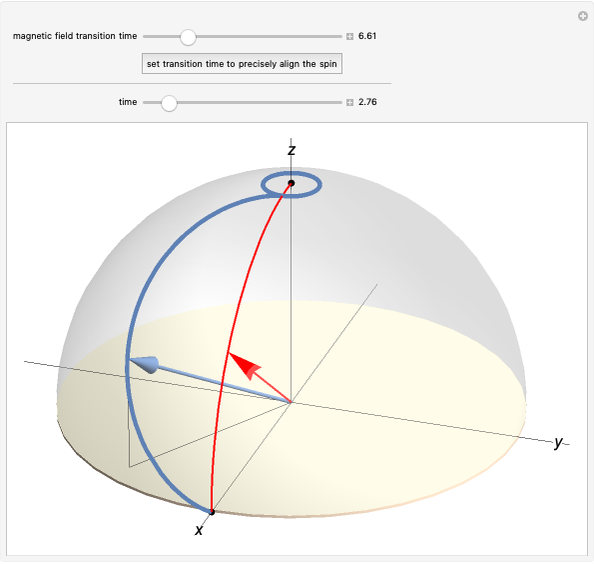
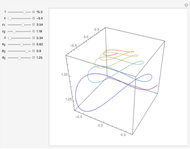
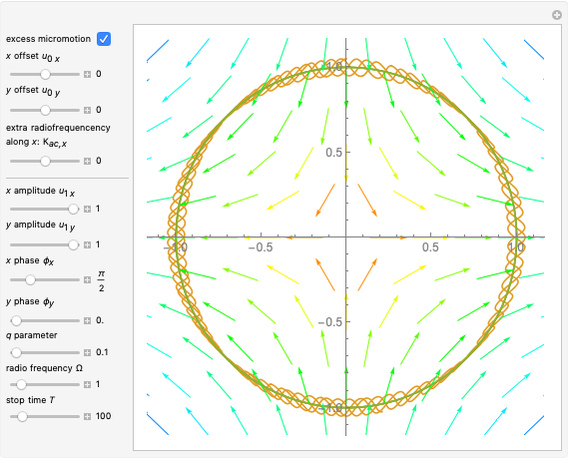
A Paul trap uses electric fields oscillating at a radiofrequency (rf)  to confine charged particles (such as ions) in space. The graphic shows the full path (in blue, only when "excess micromotion" is false) and a low-order approximation (in orange) of the motion of a single ion in a Paul trap. One of the simplest Paul traps is implemented with an oscillating quadrupole electric field. A static quadrupole vector field is shown for reference.
to confine charged particles (such as ions) in space. The graphic shows the full path (in blue, only when "excess micromotion" is false) and a low-order approximation (in orange) of the motion of a single ion in a Paul trap. One of the simplest Paul traps is implemented with an oscillating quadrupole electric field. A static quadrupole vector field is shown for reference.
Contributed by: Roland Hablützel (August 2022)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshot 1: excess micromotion due to ion displacement; the micromotion amplitude follows the local quadrupole
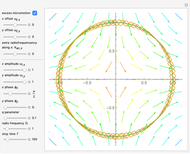
Snapshot 2: excess micromotion due to an additional oscillating term along the  direction
direction
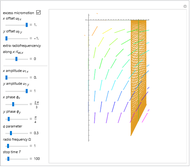
Snapshot 3: comparison of secular, low-order and full solution of the ion motion
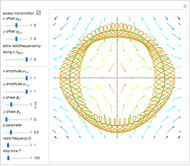
Snapshot 4: unstable orbit for 
The  factors in the
factors in the  and
and  directions are equal and opposite.
directions are equal and opposite.
A low-order approximation is not sufficient for an accurate description of the ion path for increasing values of the  parameter.
parameter.
The IonPath function is the solution of
DSolve[{ui''[t]+2q Cos[Ω t]Ω^2/4ui[t]==0,ui[-&straightpi;/ω]==u1(1+1/2q Cos[&straightpi; Ω/ω]),ui'[-&straightpi;/ω]⩵1/2q u1 Ω Sin[&straightpi; Ω/ω]},ui, t]
/. ω->Ω RealAbs[q]/(2 Sqrt[2])
Reference
[1] D. J. Berkeland, J. D. Miller, J. C. Bergquist, W. M. Itano and D. J. Wineland, "Minimization of Ion Micromotion in a Paul Trap," Journal of Applied Physics, 83(10), 1998 pp. 5025–5033. doi:10.1063/1.367318.
Permanent Citation