Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

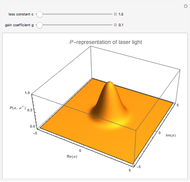
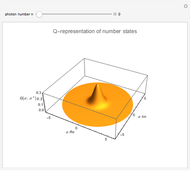
Quantum Effects in Atom-Field Interaction

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

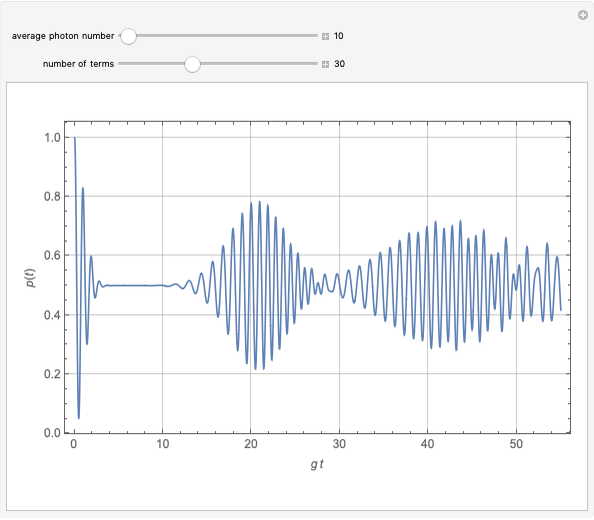
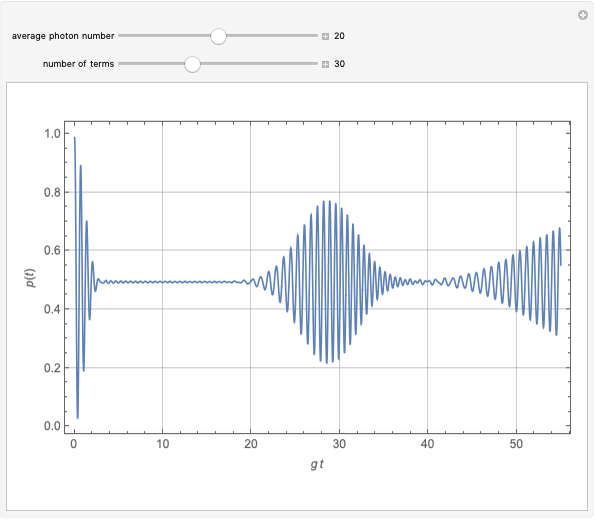
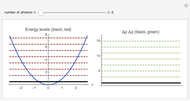
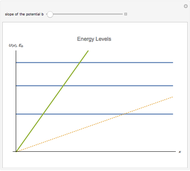
The simplest nontrivial model of the interaction between a two-level atom and a single-mode radiation field is the Jaynes–Cummings model, as follows:

[more]

The Hamiltonian is the sum of the radiation term , the atom term and the interaction . Here and are radiation and atomic frequencies, and are annihilation and creation operators of the radiation field, and , and are Pauli spin operators. The quantum equations of motion (in either the Heisenberg or Schrödinger picture) can be solved analytically.

Here the initial state of the system is taken as the atom in the excited state and the radiation field in a coherent state . We assume (corresponding to a detuning frequency of 0 between the atom and field). Then the probability to find the atom in the excited state at time is given by

.

The accuracy in approximating the infinite sum improves as the number of terms is increased.

The snapshots show evolving in time, represented by the dimensionless product . The parameter represents the expectation value of the photon number in the range 10 to 30.

[less]

Contributed by: Reinhard Tiebel (August 2022)
Open content licensed under CC BY-NC-SA

Snapshots

Details

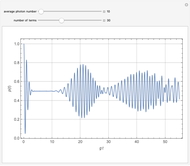
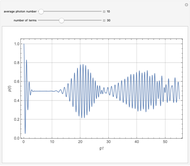
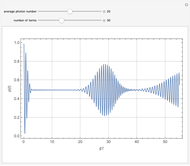
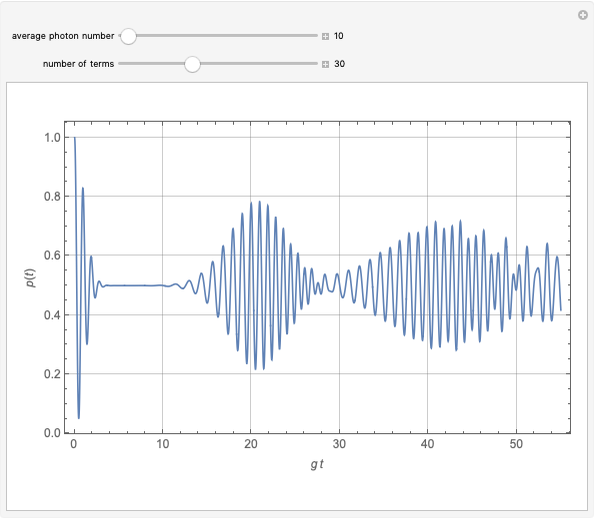
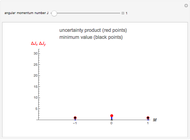
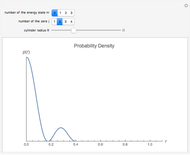
The probability distribution shows both constructive and destructive interference, as well as signal collapses and revivals. These behaviors are purely quantum effects and cannot occur in the semiclassical theory.

Rempe, Walther and Klein [3] have demonstrated collapses and revivals experimentally using a single-atom maser.

References

[1] P. Meystre, M. Sargent III, Elements of Quantum Optics, 2nd ed., Berlin: Springer–Verlag, 1991.

[2] M. O. Scully and M. S. Zubairy, Quantum Optics, New York: Cambridge University Press, 1997.

[3] G. Rempe, H. Walther and N. Klein, "Observation of Quantum Collapse and Revival in a One-Atom Maser," Physical Review Letters, 58(4), 1987 pp. 353–356. doi:10.1103/PhysRevLett.58.353.

[4] Wikipedia. "Jaynes-Cummings-Modell." (Apr 18, 2022) de.wikipedia.org/wiki/Jaynes-Cummings-Modell.

[5] Wikipedia. "Jaynes–Cummings Model." (Apr 18, 2022) en.wikipedia.org/wiki/Jaynes-Cummings_model.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send