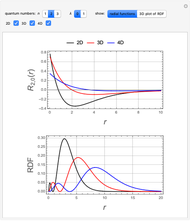
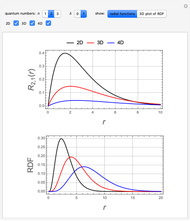
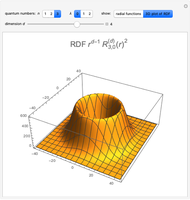
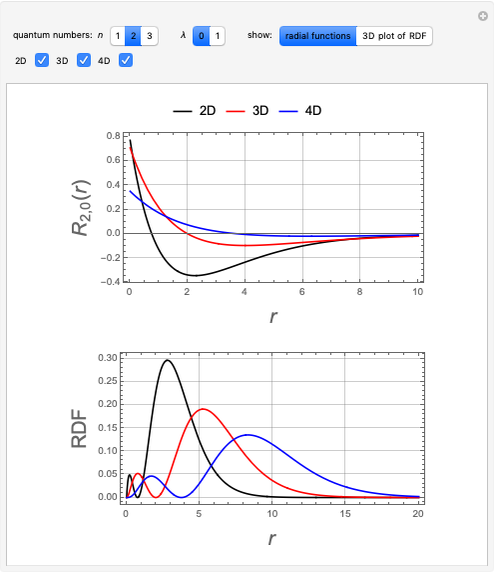
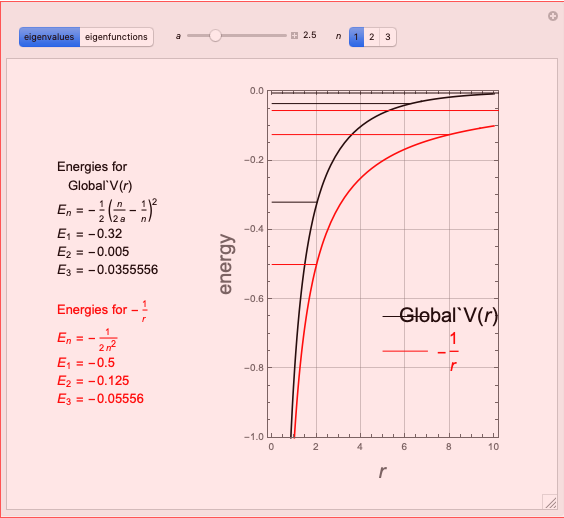
Hydrogen Atom in Varying Dimensions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
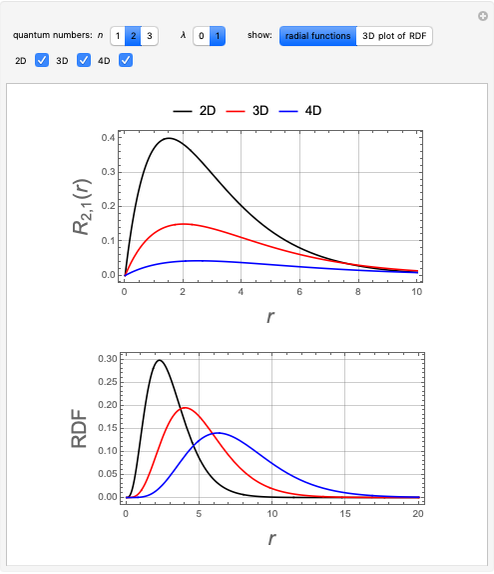
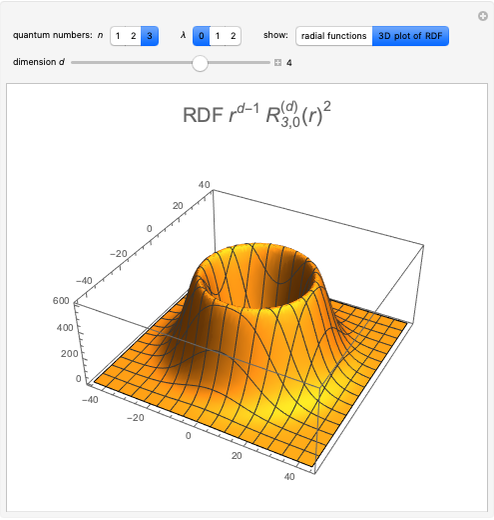
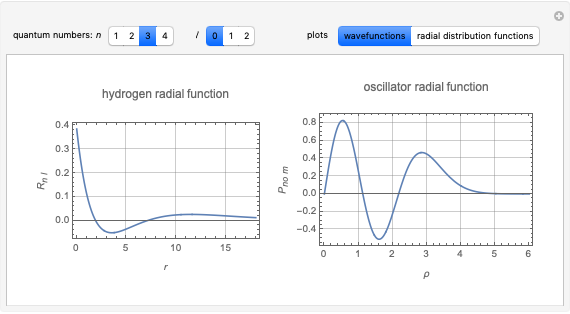
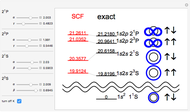
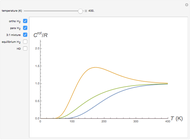
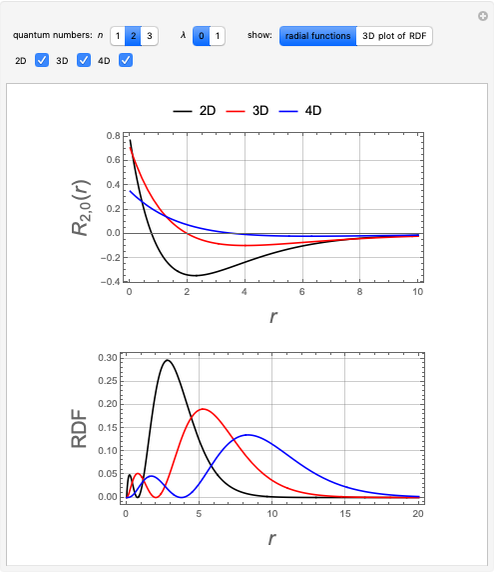
This Demonstration considers the hypothetical problem of the hydrogen atom in  -dimensional space (other than
-dimensional space (other than  ). Specifically, we consider the radial function obeying the radial Schrödinger equation in atomic units
). Specifically, we consider the radial function obeying the radial Schrödinger equation in atomic units
Contributed by: S. M. Blinder (January 2021)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The general solution of the radial differential equation can be found using DSolve. Restrictions on the values of  and
and  follow from the requirement that the Laguerre functions reduce to polynomials, in order that
follow from the requirement that the Laguerre functions reduce to polynomials, in order that  remains finite as
remains finite as  . The normalization constants can be determined using the integrals
. The normalization constants can be determined using the integrals
 .
.
The problem has been considered in [1–3].
References
[1] F. Carusoa, J. Martins and V. Oguri, "On the Existence of Hydrogen Atoms in Higher Dimensional Euclidean Spaces," Physics Letters A, 377(9), 2013 pp. 694–698. doi:10.1016/j.physleta.2013.01.026.
[2] S. M. Al-Jaber, "Hydrogen Atom in N Dimensions," International Journal of Theoretical Physics, 37(4), 1998 pp. 1289–1298. doi:10.1023/A:1026679921970.
[3] X. L. Yang, S. H. Guo, F. T. Chan, K. W. Wong and W. Y. Ching, "Analytic Solution of a Two-Dimensional Hydrogen Atom. I. Nonrelativistic Theory," Physical Review A, 43(3), 1991 pp. 1186–1196. doi:10.1103/physreva.43.1186.
Permanent Citation