Single-Component Fugacity

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
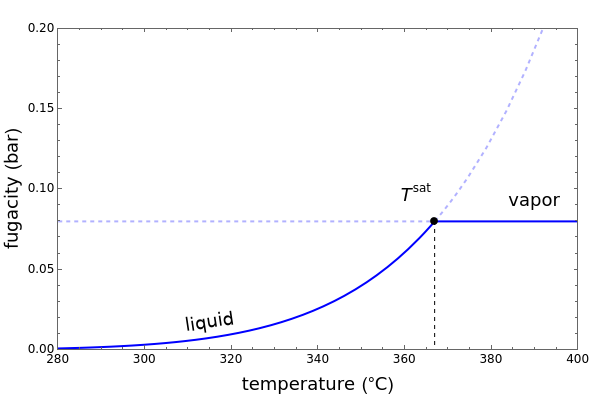
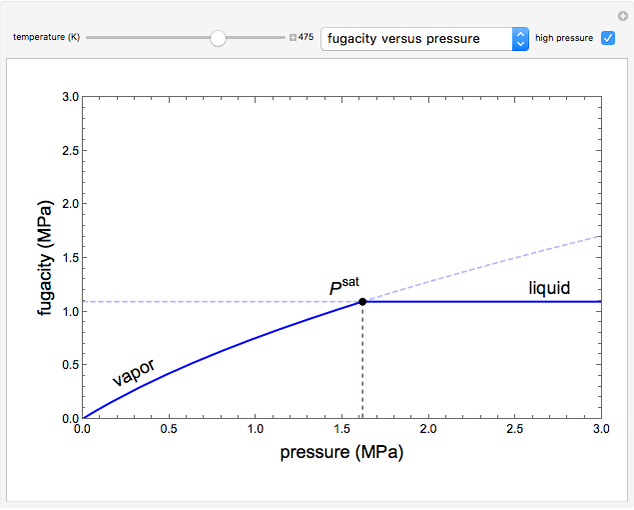
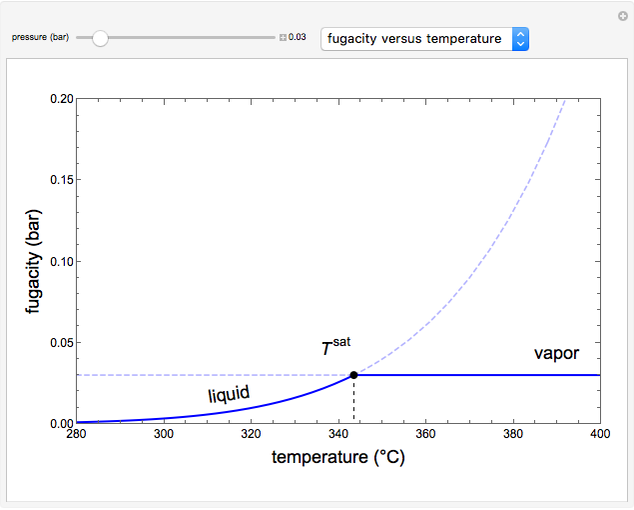
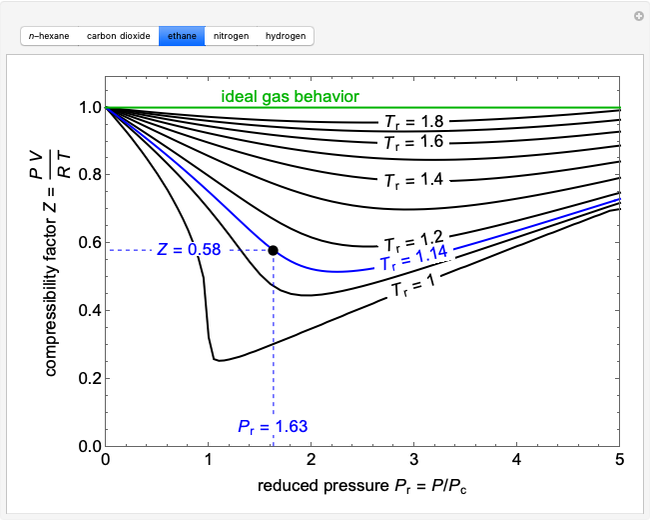
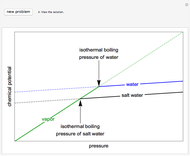
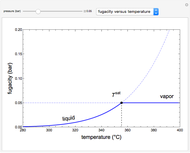
This Demonstration plots fugacity of a hypothetical single component as a function of temperature or pressure. Use the dropdown menu to select the plot.
[more]
Contributed by: Neil Hendren (October 2018)
Additional contributions by: Rachael L. Baumann and John L. Falconer
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA
Details
Fugacity is used instead of Gibbs free energy to determine phase equilibrium because it is easier to use (the fugacity of a pure-component ideal gas is the same as the pressure). Fugacity is defined by:
 (1)
(1)
where 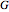 is the Gibbs energy,
is the Gibbs energy, 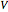 is specific volume,
is specific volume,  is pressure,
is pressure, 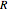 is the gas constant,
is the gas constant,  is temperature and
is temperature and 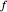 is fugacity. When two phases are in equilibrium for a single component, the fugacity of the component is the same in each phase. When only one phase exists, it is the phase with the lower fugacity.
is fugacity. When two phases are in equilibrium for a single component, the fugacity of the component is the same in each phase. When only one phase exists, it is the phase with the lower fugacity.
Equation (1) can be integrated, using the fact that the fugacity of an single-component ideal gas is the pressure, to yield:
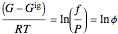 (2)
(2)
where 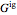 is the Gibbs energy of an ideal gas and
is the Gibbs energy of an ideal gas and  is the fugacity coefficient. Equation (2) can be applied to solids, liquids or gases. Below the critical point, the Poynting correction is used to calculate the fugacity of a liquid or solid:
is the fugacity coefficient. Equation (2) can be applied to solids, liquids or gases. Below the critical point, the Poynting correction is used to calculate the fugacity of a liquid or solid:
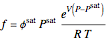 (3)
(3)
where 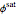 is the fugacity coefficient at saturation conditions,
is the fugacity coefficient at saturation conditions,  is the saturation pressure and
is the saturation pressure and 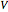 is the liquid or solid volume, which is assumed independent of pressure. For low pressure, we assume that
is the liquid or solid volume, which is assumed independent of pressure. For low pressure, we assume that
 (4)
(4)
and
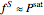 (5)
(5)
where the superscripts  and
and 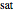 represent liquid, solid and saturation properties.
represent liquid, solid and saturation properties.
Snapshots
Permanent Citation