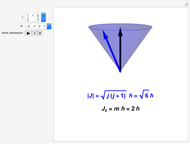
The Runge-Lenz Vector

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
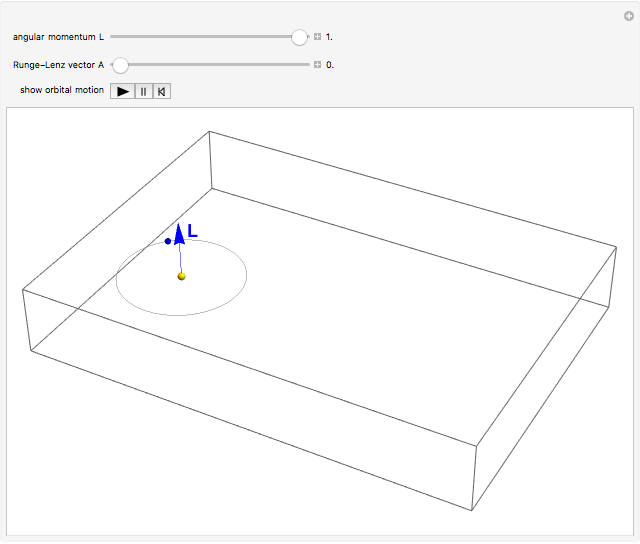
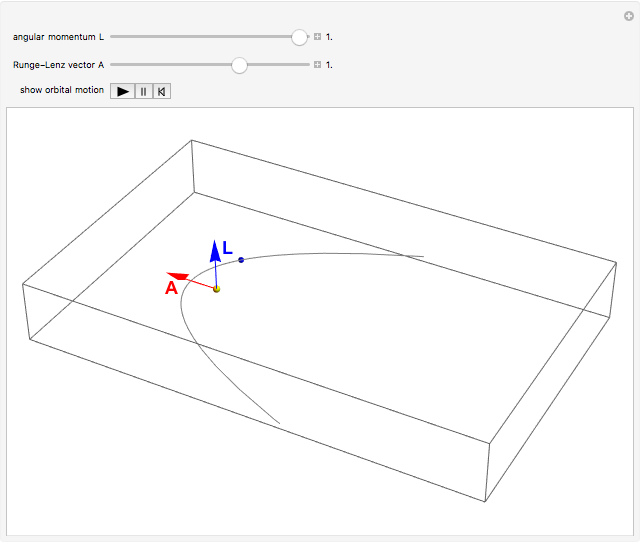
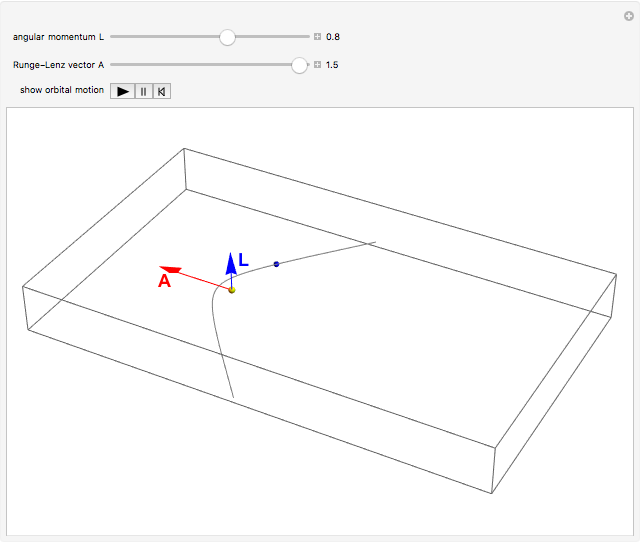
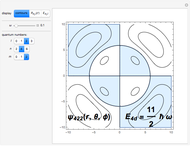
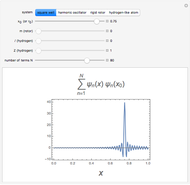
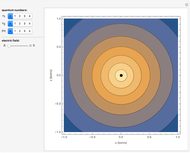
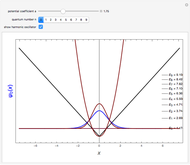
The Runge–Lenz (RL) vector, also commonly known as the Laplace–Runge–Lenz vector, is a "hidden" constant of the motion for both the classical Kepler and quantum Coulomb problems. In classical mechanics, it implies that the energy of planetary motion depends only on the semimajor axis of an elliptical orbit and is independent of the angular momentum. In quantum mechanics, it accounts for the 2 -2
-2 , 3
, 3 -3
-3 -3
-3 , and so on orbital degeneracy in the nonrelativistic hydrogen atom. As noted by Goldstein [2] and [3], this vector was actually discovered independently over the years by several other scientists, including possibly Newton himself.
, and so on orbital degeneracy in the nonrelativistic hydrogen atom. As noted by Goldstein [2] and [3], this vector was actually discovered independently over the years by several other scientists, including possibly Newton himself.
Contributed by: S. M. Blinder (August 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
See Laplace–Runge–Lenz vector.
References
[1] H. Goldstein, Classical Mechanics, 2nd ed., Reading, MA: Addison Wesley, 1980, pp. 102–105, 421–422.
[2] H. Goldstein, "Prehistory of the Runge–Lenz Vector," American Journal of Physics, 43, 1975 pp. 735–738.
[3] H. Goldstein, "More on the Prehistory of the Runge–Lenz Vector," American Journal of Physics, 44, 1976 pp. 1123–1124.
Permanent Citation