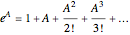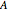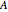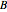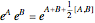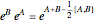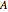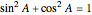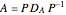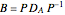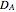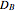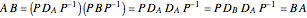Trigonometric Functions of Commutative Matrices

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
An exponential or trigonometric function 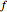 of a matrix is defined in terms of the Taylor series expansion of
of a matrix is defined in terms of the Taylor series expansion of  [2]:
[2]:
Contributed by: D. Meliga, A. Ratti and S. Z. Lavagnino (August 2019)
Additional contribution by: L. Lavagnino
Open content licensed under CC BY-NC-SA
Details
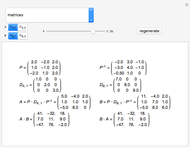
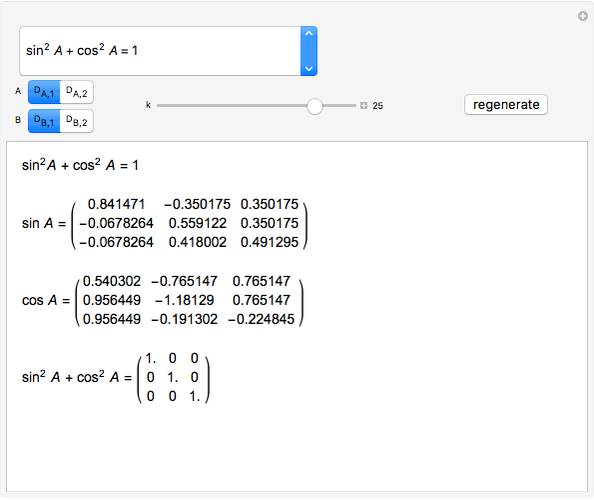
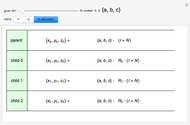
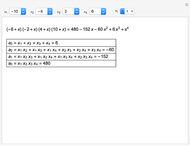
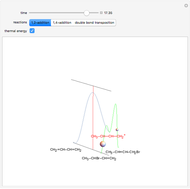
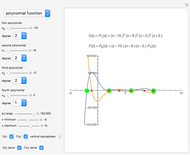
Snapshot 1: initial matrices used for all the operations
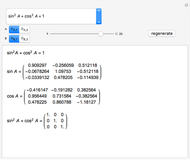
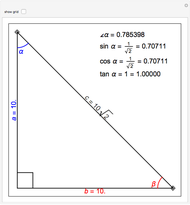
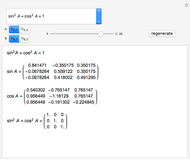
Snapshot 2: trigonometric identity applied to the  matrix
matrix
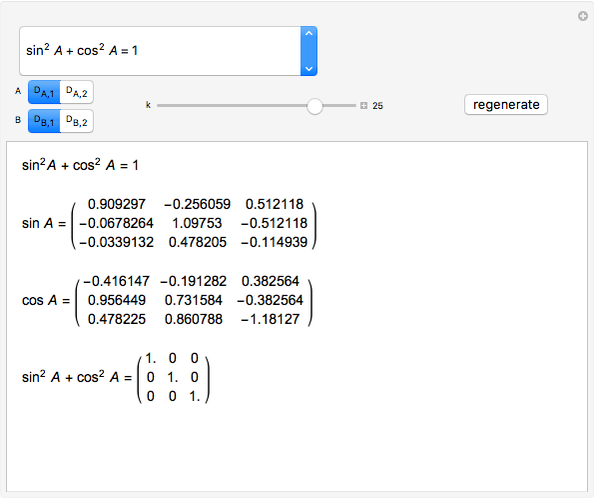
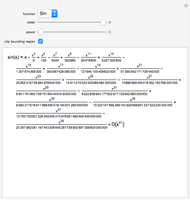
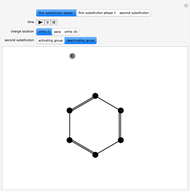
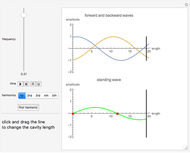
Snapshot 3: trigonometric sum to product identity applied to 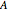 and
and 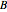 matrices with an insufficient degree of the Taylor series
matrices with an insufficient degree of the Taylor series
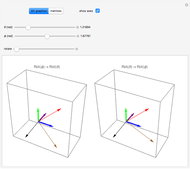
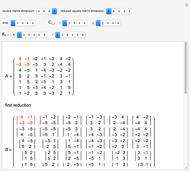
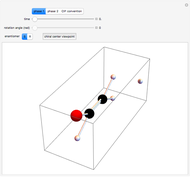
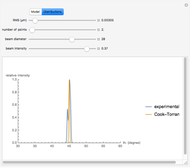
Snapshot 4: Baker–Campbell–Hausdorff formula applied to  and
and  matrices; as they commute, the formula is simplified
matrices; as they commute, the formula is simplified
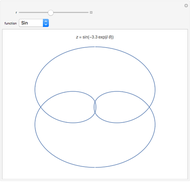
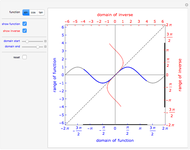
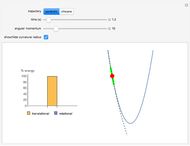
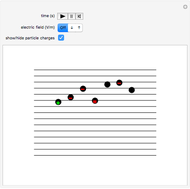
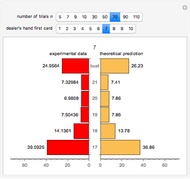
Snapshot 5: trace versus degree plot of the two trigonometric sums to product identity matrices; the two plots overlap when the degree is high enough and the identity is correct
References
[1] S. Lipschutz and M. L. Lipson, Linear Algebra, 4th ed., New York: McGraw-Hill, 2009.
[2] Wikipedia. "Trigonometric Functions of Matrices." (Jun 24, 2019) en.wikipedia.org/wiki/Trigonometric_functions_of_matrices.
[3] Wikipedia. "Baker–Campbell–Hausdorff formula." (Aug 9, 2019) en.wikipedia.org/wiki/Baker% E2 %80 %93 Campbell % E2 %80 %93 Hausdorff_formula.
Snapshots
Permanent Citation