WKB Computations on Morse Potential

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
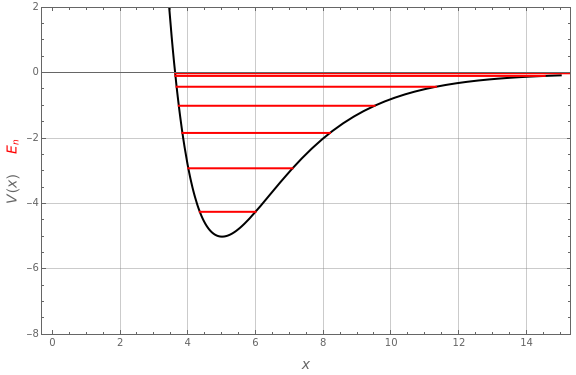
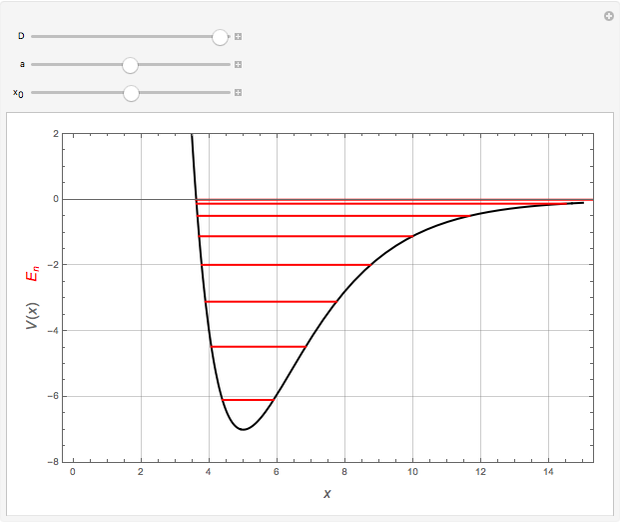
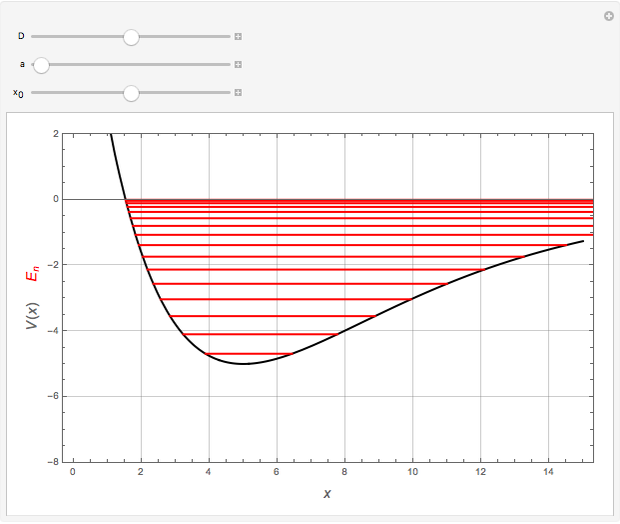
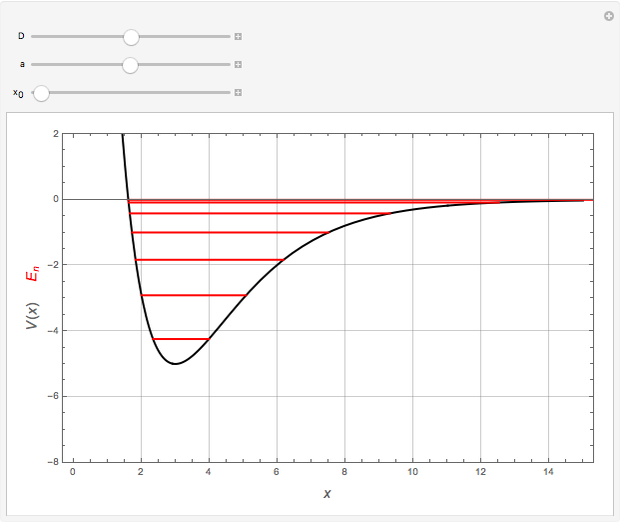
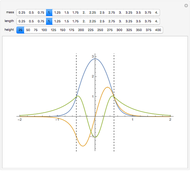
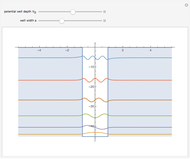
The semiclassical Wentzel–Kramers–Brillouin (WKB) method applied to one-dimensional problems with bound states often reduces to the Sommerfeld–Wilson quantization conditions, the cyclic phase-space integrals  . It turns out that this formula gives the exact bound-state energies for the Morse oscillator with
. It turns out that this formula gives the exact bound-state energies for the Morse oscillator with  . The requisite integral can be reduced to
. The requisite integral can be reduced to  , in which
, in which  and
and  are the classical turning points
are the classical turning points  . The integral can be done "by hand", using the transformation
. The integral can be done "by hand", using the transformation  followed by a contour integration in the complex plane, but Mathematica can evaluate the integral explicitly, needing only the additional fact that
followed by a contour integration in the complex plane, but Mathematica can evaluate the integral explicitly, needing only the additional fact that  The result reads
The result reads
 , which can be solved for
, which can be solved for  to give
to give  ,
,  , in units with
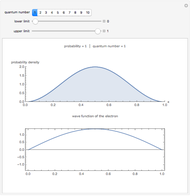
, in units with  . The highest bound state is given by
. The highest bound state is given by  , where
, where  represents the floor, which for positive numbers is simply the integer part. The values of
represents the floor, which for positive numbers is simply the integer part. The values of  ,
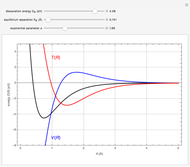
,  , and
, and  (expressed in atomic units) used in this Demonstration are for illustrative purposes only and are not necessarily representative of any actual diatomic molecule.
(expressed in atomic units) used in this Demonstration are for illustrative purposes only and are not necessarily representative of any actual diatomic molecule.
Contributed by: S. M. Blinder (January 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
A particle in a one-dimensional potential can be described by the Schrödinger equation:  .
.
The semiclassical or WKB method is based on the ansatz  . In the limit as
. In the limit as  ,
,  in the exponential satisfies the Hamilton–Jacobi equation for the action function
in the exponential satisfies the Hamilton–Jacobi equation for the action function  , with one solution
, with one solution  . It is then shown in most graduate-level texts on quantum mechanics (e.g. Schiff, Merzbacher, etc.) that this usually leads to the Sommerfeld–Wilson quantum conditions on periodic orbits
. It is then shown in most graduate-level texts on quantum mechanics (e.g. Schiff, Merzbacher, etc.) that this usually leads to the Sommerfeld–Wilson quantum conditions on periodic orbits  ,
,  . For one-dimensional problems, the cyclic integral can be replaced by
. For one-dimensional problems, the cyclic integral can be replaced by  , where
, where  ,
,  are the classical turning points of the motion and
are the classical turning points of the motion and  .
.
As an étude consider the linear harmonic oscillator, with  and
and  . The quantum condition reads
. The quantum condition reads  , which can be solved to give
, which can be solved to give  . This is one of a small number of cases in which the WKB method gives the exact quantum-mechanical energies.
. This is one of a small number of cases in which the WKB method gives the exact quantum-mechanical energies.
Permanent Citation