Assessing Total Risk from Interacting Factors

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
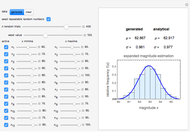
Risk assessment models are based mainly on the notion that the effects of factors are either additive or multiplicative. Theoretically, at least, risk factors can interact in other ways. This Demonstration provides hypothetical examples of the risk defined by three different kinds of models of increasing complexity and number of factors. Assuming that the factors can be identified, their interactions described by an algebraic model, and their lower and upper limits specified, the "best risk estimate" is reached by a Monte Carlo simulation method akin to the "expanded Fermi solution". The best estimate can be extracted directly from the generated risk estimates' histogram or calculated as the mode of a superimposed normal or lognormal distribution function for comparison.
Contributed by: Mark D. Normand and Micha Peleg (October 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
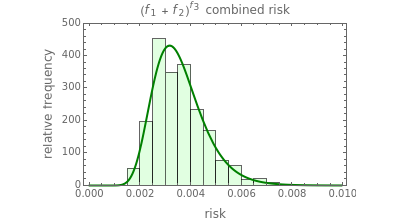
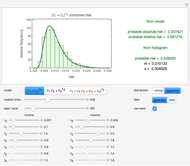
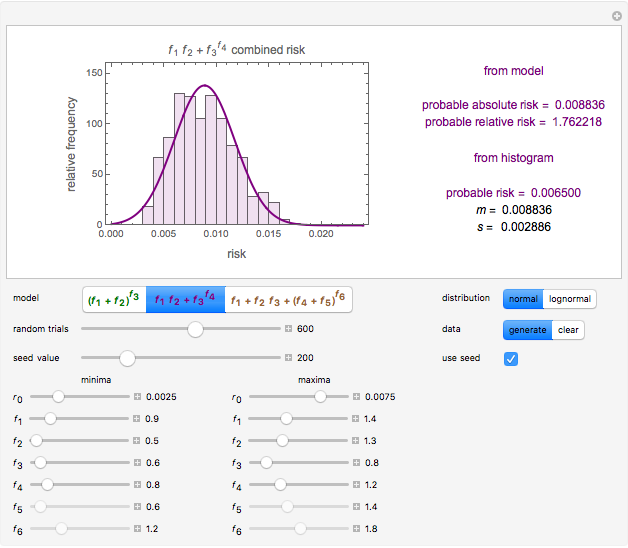
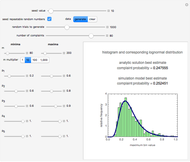
Snapshot 1: Risk of three hypothetical interacting factors following model 1 with a lognormal distribution superimposed on the estimates' histogram
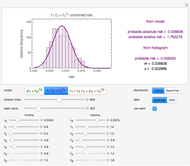
Snapshot 2: Risk of four hypothetical interacting factors following model 2 with a normal distribution superimposed on the estimates' histogram
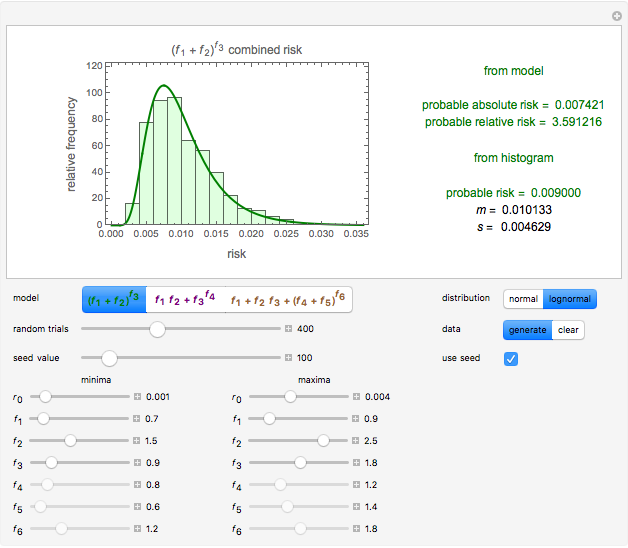
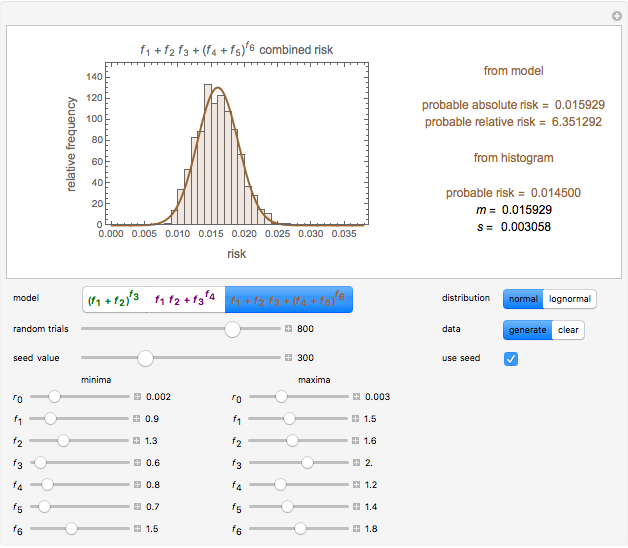
Snapshot 3: Risk of six hypothetical interacting factors following model 3 with a normal distribution superimposed on the estimates' histogram
The combined risk of additive and multiplicative factors specified by their ranges can be calculated analytically or estimated by Monte Carlo simulations in which the estimates' distribution is approximately normal or lognormal as anticipated by the central limit theorem [1, 2]. This Demonstration generates combined risks with three purely hypothetical interactive models that are neither purely additive nor purely multiplicative. These models' parameters are specified by their assumed ranges, as entered by the user. The most probable combined risk is either calculated by the expanded Fermi solution method [1] or determined directly from the generated estimates' histogram. It is assumed [2] that there is a baseline risk, 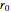 , whose lower and upper limits are entered with sliders, and three to six interacting risk factors,
, whose lower and upper limits are entered with sliders, and three to six interacting risk factors,  to
to  , depending on the model, whose lower and upper limits are also entered with sliders.
, depending on the model, whose lower and upper limits are also entered with sliders.
For the three models, the absolute risk is defined as  ,
,  , or
, or 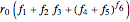 , and the relative risk as the corresponding
, and the relative risk as the corresponding 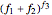 ,
, 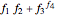 , or
, or 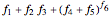 , respectively. The program generates a number of estimates using the selected model's equation with random values of the terms within their respective specified ranges, plots their histogram, and shows the numeric values of their mean (
, respectively. The program generates a number of estimates using the selected model's equation with random values of the terms within their respective specified ranges, plots their histogram, and shows the numeric values of their mean ( ) and standard deviation (
) and standard deviation ( ). Superimposed on the histogram is the PDF of a normal or lognormal distribution, having the same linear or logarithmic mean and standard deviation as the generated data, respectively.
). Superimposed on the histogram is the PDF of a normal or lognormal distribution, having the same linear or logarithmic mean and standard deviation as the generated data, respectively.
The probable absolute risk can also be identified as the center value of the highest bin in the histogram or the mode of the corresponding normal or lognormal distribution, for comparison. The probable relative risk is similarly calculated, except that no histogram is created. The user can clear the data and generate a new set, and fix or leave unknown the seed for the Monte Carlo simulations.
The magnitude of the 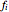 can be used to account for risk elevation or reduction. A factor's limits, for example,
can be used to account for risk elevation or reduction. A factor's limits, for example, 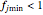 and
and 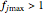 , can account for uncertainties in whether their effect is beneficial or harmful. None of the scenarios created by the Demonstration have been intended to simulate a specific real-life risk. The Demonstration's sole purpose is to show that the expanded Fermi solution method can be extended to situations where, unlike in the cases of additive and multiplicative risks, there is no obvious analytical solution or expected distribution based on theoretical considerations.
, can account for uncertainties in whether their effect is beneficial or harmful. None of the scenarios created by the Demonstration have been intended to simulate a specific real-life risk. The Demonstration's sole purpose is to show that the expanded Fermi solution method can be extended to situations where, unlike in the cases of additive and multiplicative risks, there is no obvious analytical solution or expected distribution based on theoretical considerations.
References
[1] M. Peleg, M. D. Normand, J. Horowitz, and M. G. Corradini, "An Expanded Fermi Solution for Microbial Risk Assessment," International Journal of Food Microbiology, 113(1), 2007 pp. 92–101. doi:10.1016/j.ijfoodmicro.2006.07.020.
[2] M. Peleg, M. D. Normand, and M. G. Corradini, "A Method to Estimate a Person or Group Health Risks and Benefits from Additive and Multiplicative Factors," Trends in Food Science and Technology, forthcoming. doi:10.1016/j.tifs.2012.05.003.
Permanent Citation