Distribution of a Robot Swarm in a Square under Gravity

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
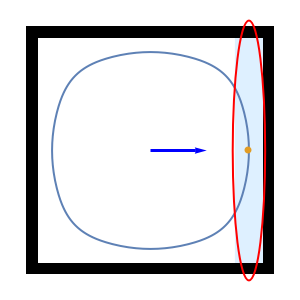
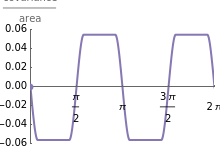
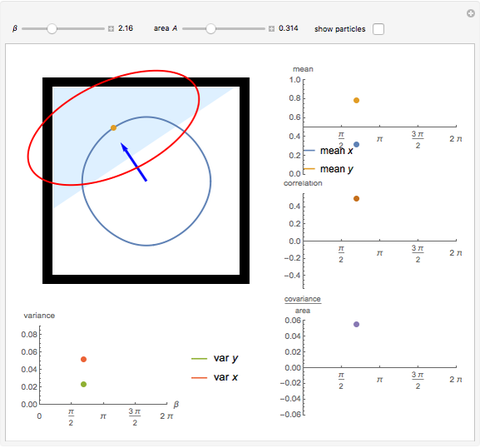
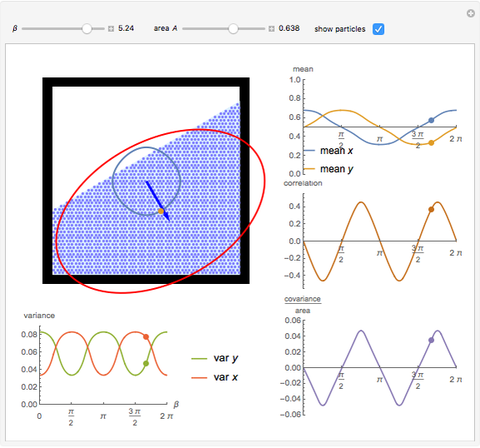
This Demonstration determines the mean, variance, and covariance for a very large swarm of robots as they move inside a square workplace under the influence of gravity, pointing in the direction  . The swarm is large, but the robots are comparatively small and together cover a constant area
. The swarm is large, but the robots are comparatively small and together cover a constant area  . Under gravity, they flow like a liquid, moving to one side of the workplace to form a polygonal shape.
. Under gravity, they flow like a liquid, moving to one side of the workplace to form a polygonal shape.
Contributed by: Haoran Zhao and Aaron T. Becker (January 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The direction of the force of gravity is determined by the angle  , in
, in  , such that the swarm can assume eight different polygonal shapes. The shapes alternate between triangles and trapezoids when
, such that the swarm can assume eight different polygonal shapes. The shapes alternate between triangles and trapezoids when 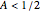 , and alternate between squares with one corner removed and trapezoids when
, and alternate between squares with one corner removed and trapezoids when  .
.
Computing the means  and
and  , variances
, variances 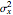 and
and 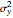 , covariance
, covariance 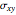 , and correlation
, and correlation 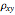 requires integration over the area containing the swarm. One way is to use an indicator function
requires integration over the area containing the swarm. One way is to use an indicator function 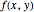 that returns 1 if the point
that returns 1 if the point 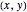 is inside the region containing the swarm and 0 otherwise. The formulas are as follows, integrating over the unit square with
is inside the region containing the swarm and 0 otherwise. The formulas are as follows, integrating over the unit square with  and
and  from 0 to 1.
from 0 to 1.
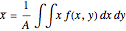 ,
,  ,
,
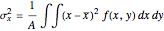 ,
,  ,
,
 ,
,
 .
.
Instead of using an indicator function, the region of integration can be changed to only include the polygon containing the swarm. As an example calculation, if the force angle is  , the mean when the swarm is in the lower-left corner is
, the mean when the swarm is in the lower-left corner is
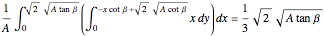 for
for  and
and  for
for  .
.
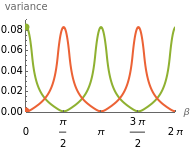
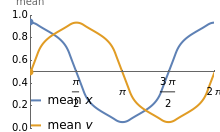
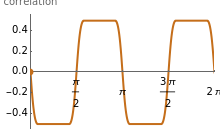
A few interesting results: the correlation is maximized when the swarm has a triangular shape, and equals 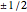 . The covariance of the triangle is always
. The covariance of the triangle is always  . Variance is maximized in one direction and minimized in the other when the swarm is in a rectangular position. Mean positions are maximized when
. Variance is maximized in one direction and minimized in the other when the swarm is in a rectangular position. Mean positions are maximized when  is small.
is small.
Permanent Citation