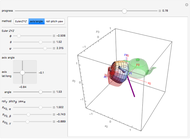
Robot Manipulator Workspaces

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
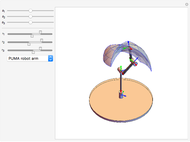
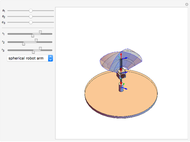
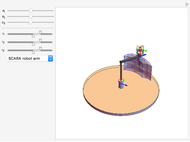
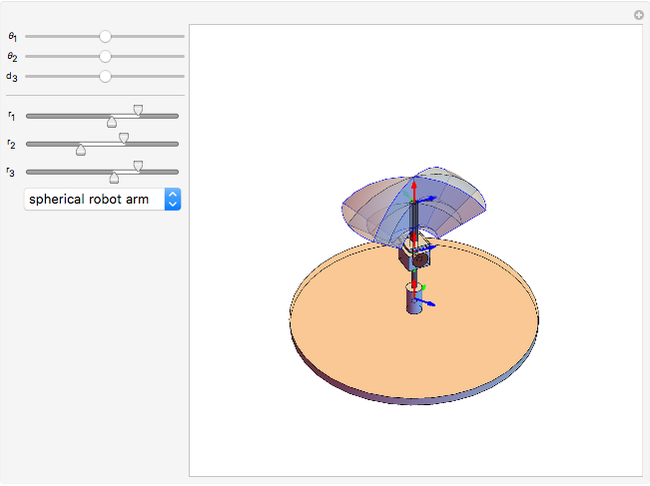
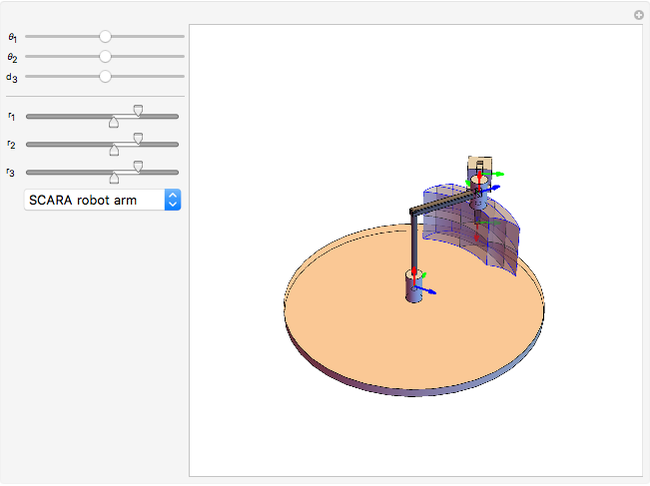
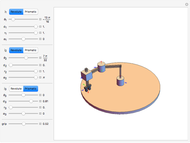
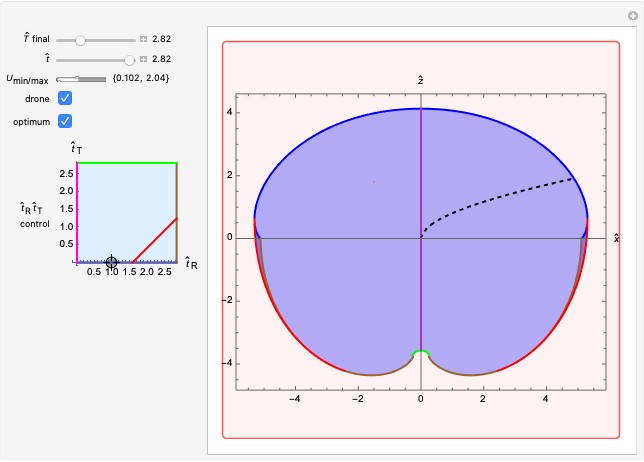
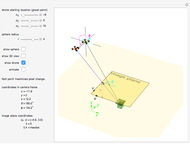
A robot's workspace is the total volume swept out by the end effector as the manipulator executes all possible motions. The shape of the workspace dictates the applications for which each design can be used. This Demonstration lets you load several robot designs to compare their workspaces. You can set the position and range for each joint using sliders.
Contributed by: Aaron T. Becker, Benedict Isichei, Muhammad Sultan and Maruthi S. Chemudupati (December 2017)
Open content licensed under CC BY-NC-SA
Details
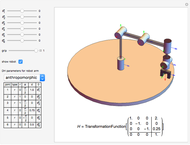
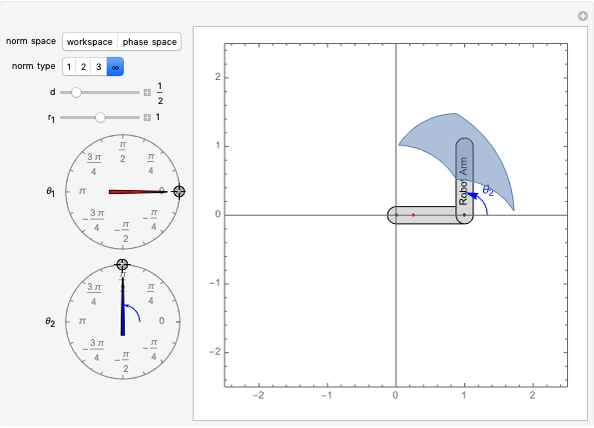
This Demonstration creates a serial-link robot arm with three joints (three degrees of freedom) and displays the robot workspace (the volume swept out by the end effector as the manipulator executes all possible motions). You can manipulate each joint using the sliders and select from a variety of robot types. The workspaces vary greatly and determine the tasks the robot is suited for.
In this Demonstration, prismatic joints and revolute joints are limited by the range sliders 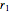 ,
, and
and 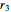 . The range is between
. The range is between 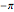 and
and  . Changes to these range sliders or to the type of robot require recomputing the workspace, which is time-consuming. Changing the current position of the robot arm updates the graphic quickly.
. Changes to these range sliders or to the type of robot require recomputing the workspace, which is time-consuming. Changing the current position of the robot arm updates the graphic quickly.
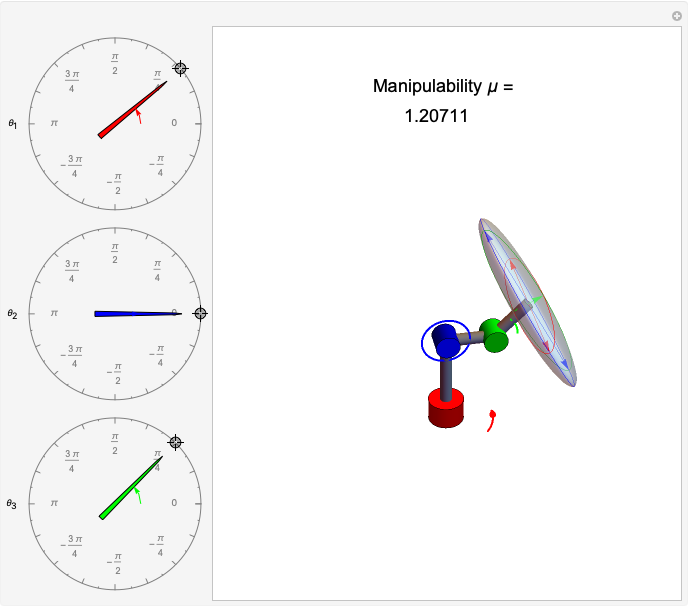
The shape of the workspace also indicates where the robots experience Jacobian singularities. Snapshot 1 shows the spherical manipulator at its default position, with the end effector pointing along the  axis. The manipulator can generate instantaneous motion in the
axis. The manipulator can generate instantaneous motion in the 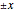 (blue arrow) and
(blue arrow) and 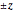 (red arrow) axes but cannot move along the
(red arrow) axes but cannot move along the 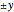 (green arrow) axis.
(green arrow) axis.
The workspaces are generated by combining multiple 2D parametric plots. These plots correspond to the parameter 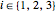 being set to its minimum, middle and maximum values, while the other parameters vary along their full ranges. For the Cartesian manipulator, this results in a cube that is divided into eight smaller cubes. For other types of robots, for instance the Stanford robot arm, the relation is less intuitive.
being set to its minimum, middle and maximum values, while the other parameters vary along their full ranges. For the Cartesian manipulator, this results in a cube that is divided into eight smaller cubes. For other types of robots, for instance the Stanford robot arm, the relation is less intuitive.
Reference
[1] M. W. Spong, S. Hutchinson and M. Vidyasagar, Robot Modeling and Control, Hoboken, NJ: John Wiley and Sons, 2006.
Snapshots
Permanent Citation