Spreading Particles in a Disk

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
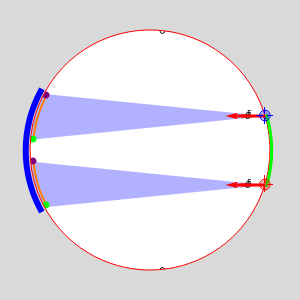
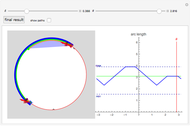
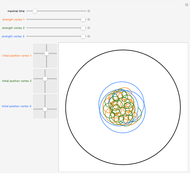
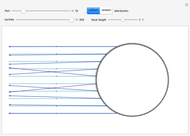
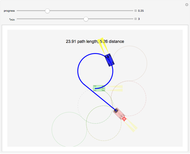
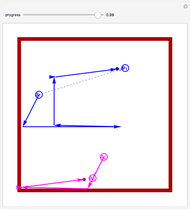
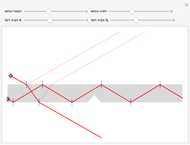
This Demonstration shows particles spreading inside a disk workspace. These might, for example, be magnetized particles inside a Petri dish pushed by an external magnetic field. The particles start along the green arc, bounded by red and blue locators. The propagated particles are pushed in the direction of  and are incident along the arc drawn in blue. Often particles cannot be controlled perfectly, which is modeled by specifying an angular spread
and are incident along the arc drawn in blue. Often particles cannot be controlled perfectly, which is modeled by specifying an angular spread  to either side of
to either side of  . This Demonstration shows the maximum and minimum particle spread (arc length) into which the particles can be manipulated.
. This Demonstration shows the maximum and minimum particle spread (arc length) into which the particles can be manipulated.
Contributed by: Daniel Bao, Tate Song and Aaron T. Becker (September 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
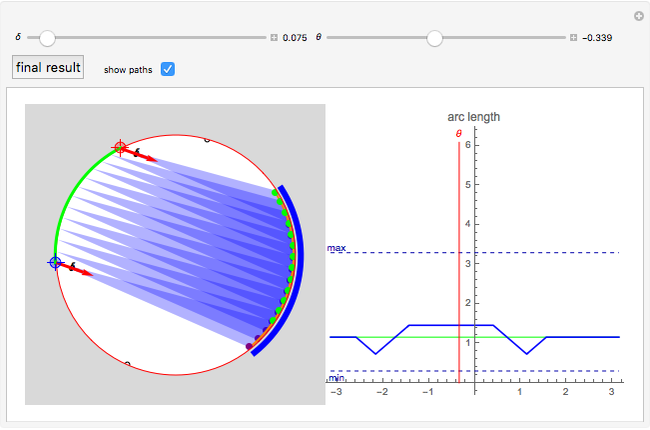
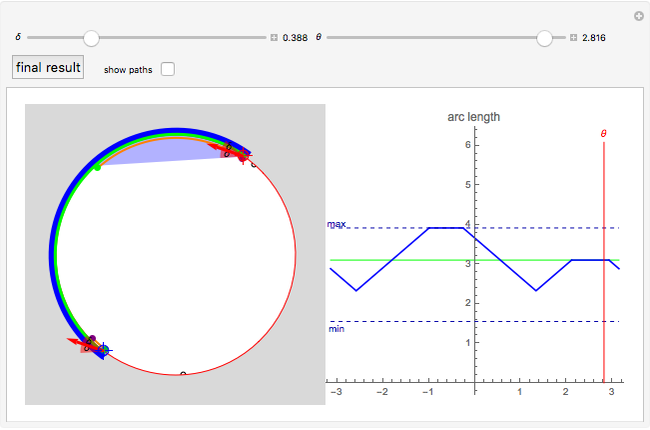
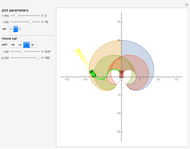
We assume a global input such that the particles start in an arc along the right side of the disk. The left-hand image shows the particle distribution in green as they propagate in the  direction, as is shown in blue. The
direction, as is shown in blue. The  direction is indicated by two red arrows, each starting from either the left or right endpoint of the arc. The particle dispersion
direction is indicated by two red arrows, each starting from either the left or right endpoint of the arc. The particle dispersion  is shown with transparent circle sectors, and the path from their current position to an ending arc is shown with a transparent blue sector, which ends along an orange arc whose extent is highlighted by green and purple points. If "show paths" is checked, additional starting points along the current arc are shown.
is shown with transparent circle sectors, and the path from their current position to an ending arc is shown with a transparent blue sector, which ends along an orange arc whose extent is highlighted by green and purple points. If "show paths" is checked, additional starting points along the current arc are shown.
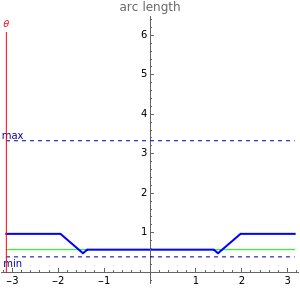
The arc length may be initialized from 0 to  radians.
radians.
Any initial distribution can be steered to a minimum arc length of  and a maximum arc length of
and a maximum arc length of  . Once the arc length exceeds the minimum, it can never be reduced to less than
. Once the arc length exceeds the minimum, it can never be reduced to less than  . Similarly, if the arc length is ever less than the maximum, it can never be increased to more than
. Similarly, if the arc length is ever less than the maximum, it can never be increased to more than  .
.
Every propagation step can add no more than  to the arc length or decrease the arc length by
to the arc length or decrease the arc length by  .
.
This Demonstration was inspired by a similar problem in polygonal workspaces by Lewis and O'Kane [1].
Reference
[1] J. S. Lewis and J. M. O'Kane, "Planning for Provably Reliable Navigation Using an Unreliable, Nearly Sensorless Robot," The International Journal of Robotics Research, 32(11), 2013 pp. 1339–1354. doi:10.1177/0278364913488428.
Permanent Citation