Distributions of Continuous Order Statistics

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Let 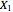 , ...,
, ...,  be a random sample from a continuous distribution. Reorder the sample in increasing order; denote the corresponding variables by
be a random sample from a continuous distribution. Reorder the sample in increasing order; denote the corresponding variables by 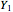 , ...,
, ..., 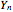 . Thus, for example,
. Thus, for example, 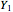 is the smallest of the
is the smallest of the 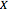 variables,
variables, 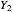 the second smallest, and
the second smallest, and 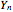 the largest. The variable
the largest. The variable  is called the
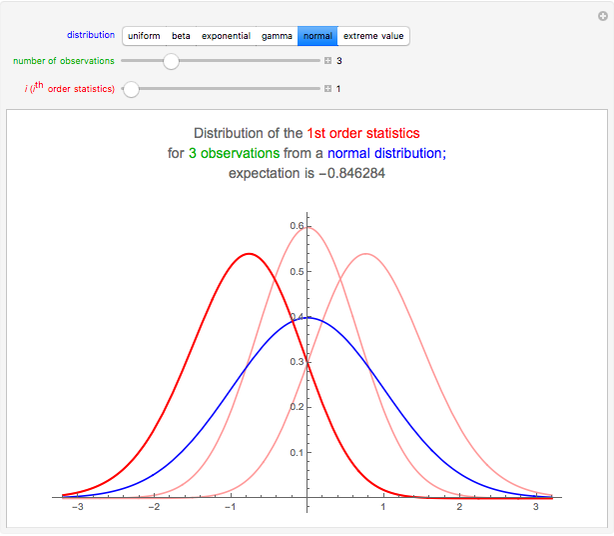
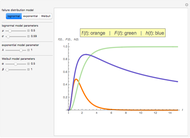
is called the 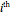 order statistic. The Demonstration shows the probabilities of the order statistics (the red curves) when the sample is from a uniform, beta, exponential, gamma, normal, or extreme value distribution (the probability density function of
order statistic. The Demonstration shows the probabilities of the order statistics (the red curves) when the sample is from a uniform, beta, exponential, gamma, normal, or extreme value distribution (the probability density function of 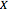 is shown in blue).
is shown in blue).
Contributed by: Heikki Ruskeepää (May 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
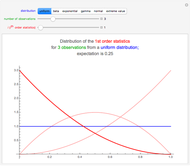
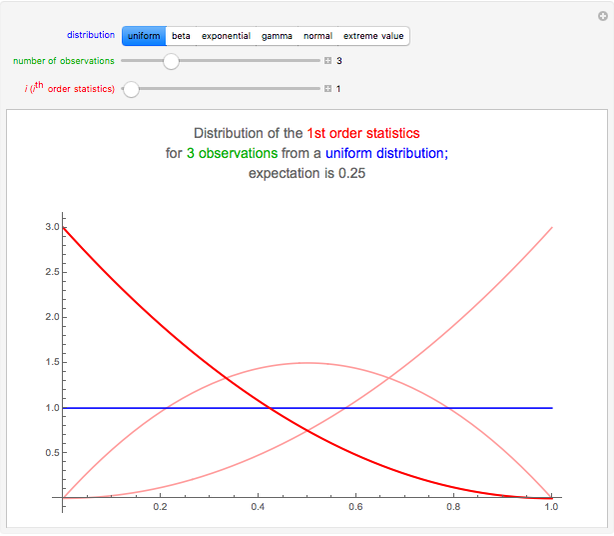
Snapshot 1: The data has the uniform distribution in the interval  ; see the blue curve. The smallest, middle, and largest result are, with high probability, in the intervals, say,
; see the blue curve. The smallest, middle, and largest result are, with high probability, in the intervals, say,  ,
, 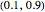 , and
, and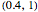 , respectively. The expectations of the smallest, middle, and largest result are 0.25, 0.5, and 0.75, respectively.
, respectively. The expectations of the smallest, middle, and largest result are 0.25, 0.5, and 0.75, respectively.
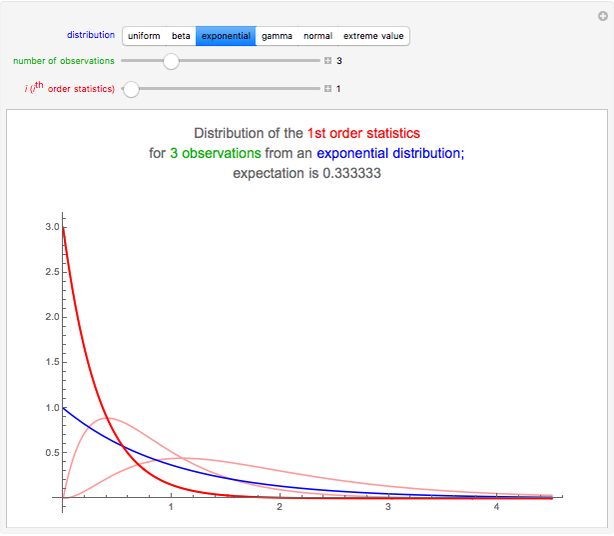
Snapshot 2: The data has the exponential distribution with expectation 1; see the blue curve. The smallest, middle, and largest result are, with high probability, at most, say, 1, 2, and 4, respectively. The expectations of the smallest, middle, and largest result are 0.33, 0.83, and 1.83, respectively.
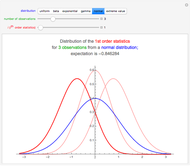
Snapshot 3: The data has the standard normal distribution with expectation 0 and standard deviation 1; see the blue curve. The smallest, middle, and largest result are, with high probability, in the intervals, say,  ,
, 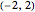 , and
, and 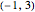 , respectively. The expectations of the smallest, middle, and largest result are -0.85, 0.0, and 0.85, respectively.
, respectively. The expectations of the smallest, middle, and largest result are -0.85, 0.0, and 0.85, respectively.
The other three distributions considered in this Demonstration are the beta distribution with parameters 3 and 2, the gamma distribution with parameters 3 and 2, and the extreme value distribution with parameters 0 and 2.
Let the probability density function and the cumulative distribution function of the data variable 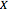 be
be 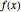 and
and  , respectively. The probability density function of the
, respectively. The probability density function of the 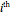 order statistics is then [1, p. 10]
order statistics is then [1, p. 10]
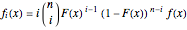 .
.
The expectations of the order statistics are calculated in the traditional way, by integrating the product of  and the density function.
and the density function.
The order statistics for several continuous distributions are considered in [1, Chapter 4].
Reference
[1] B. C. Arnold, N. Balakrishnan, and H. N. Nagaraja, A First Course in Order Statistics, Philadelphia: SIAM, 2008.
Permanent Citation