Spin Game

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
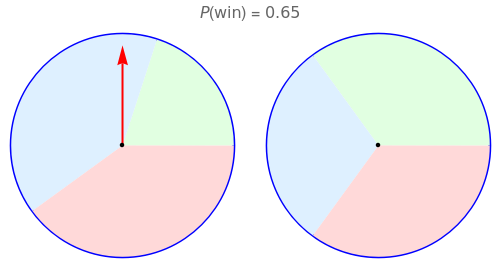
A player spins the pointers on two disks as follows. The game starts with the first disk. If the pointer stops:
[more]
Contributed by: Heikki Ruskeepää (June 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
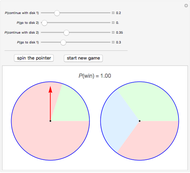
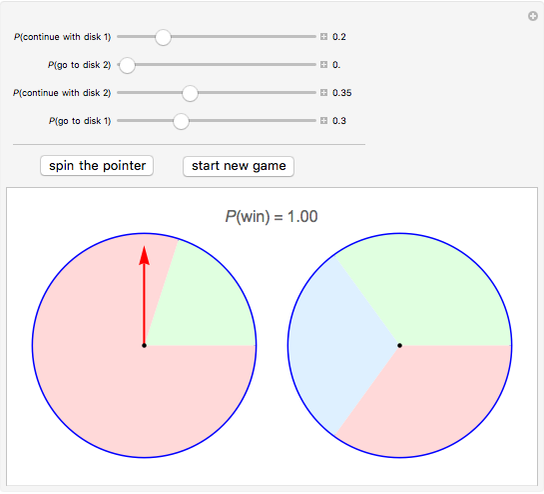
Snapshot 1: if the probability of moving from disk 1 to disk 2 is zero, the probability of winning is 1
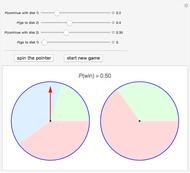
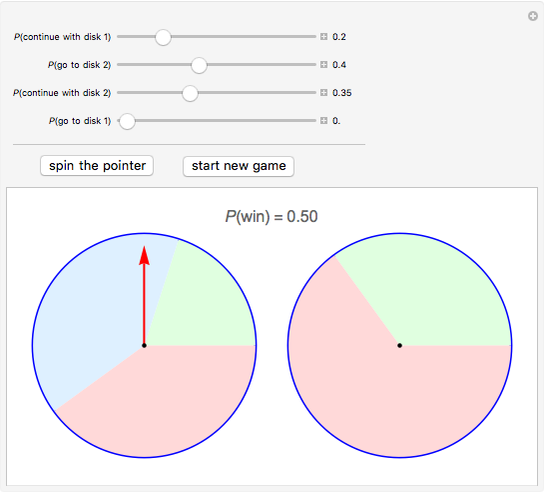
Snapshot 2: if the probability of moving from disk 2 to disk 1 is zero, the probability of winning does not depend on the probability of continuing with disk 2
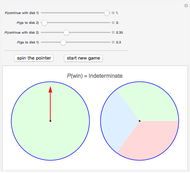
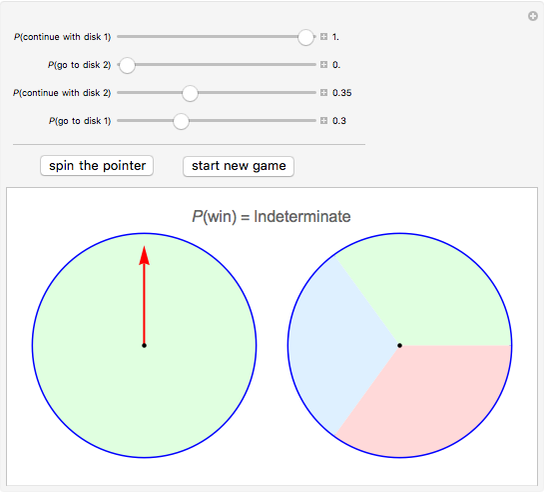
Snapshot 3: if we always continue with disk 1, the probability of winning is indeterminate because the game never ends
Snapshot 4: if we always continue with disk 2, the probability of winning is likewise indeterminate because it is possible that the game never ends
Snapshot 5: if we always move from disk 1 to disk 2 and from disk 2 to disk 1, the probability of winning is again indeterminate, because the game never ends
The Demonstration is based on [1, pp. 28, 244–247], where the probability of winning the spin game is calculated by a clever method (note the misprint in the boxed probability on p. 245: 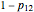 in the denominator should be
in the denominator should be  ).
).
Reference
[1] P. J. Nahin, Digital Dice: Computational Solutions to Practical Probability Problems, Princeton, NJ: Princeton University Press, 2008.
Permanent Citation
"Spin Game"
http://demonstrations.wolfram.com/SpinGame/
Wolfram Demonstrations Project
Published: June 17 2013