Walking Randomly Until No Shoes Are Available

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
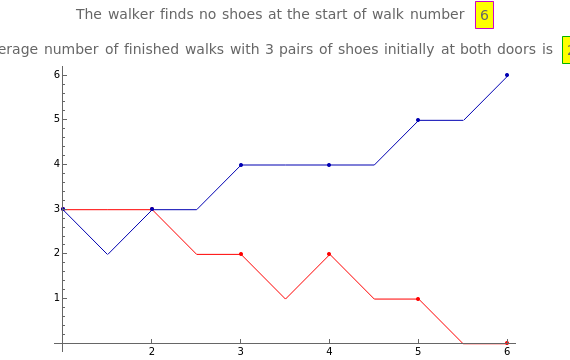
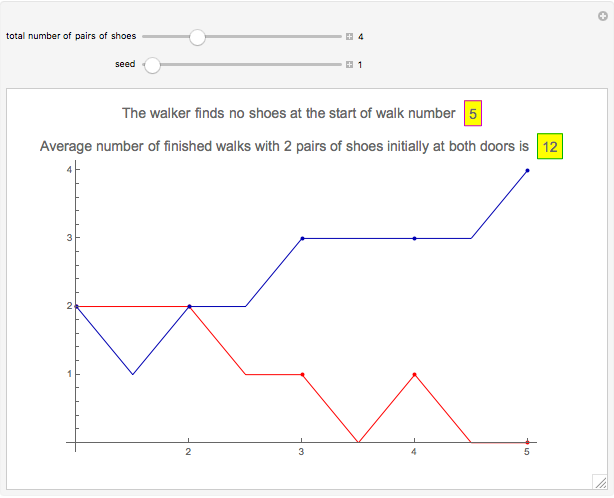
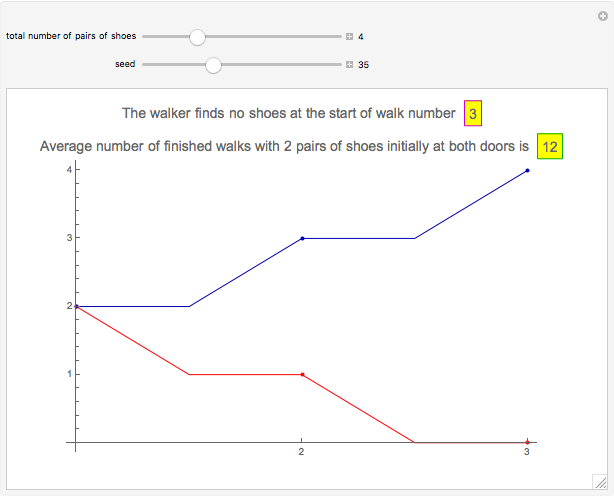
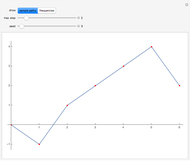
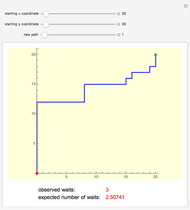
Mr. A lives in a house with one front door and one back door. Initially, he places the same number of pairs of walking shoes at each door. Then, every time he wants to go for a walk, he chooses one door at random and puts on a pair of shoes. When he returns, he again chooses a door at random and leaves his shoes at the door. Sooner or later he discovers that no shoes are available at the door that he has chosen for the next walk. This Demonstration shows simulations of this process until Mr. A finds no shoes. The red and blue curves show the number of pairs of shoes at the front and back door, respectively.
Contributed by: Heikki Ruskeepää (January 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshot 1: There are four pairs of shoes. Initially, two of them are at the front door and two at the back door. In the first walk, Mr. A happens to start at the back door (the number of pairs of shoes at the back door drops to 1, as the blue curve shows), and he also happens to stop at the back door (the number of pairs of shoes at the back door goes back to 2). In the second walk, Mr. A happens to start at the front door (the number of pairs of shoes at the front door drops to 1, as the red curve shows), and he happens to stop at the back door (the number of pairs of shoes at the back door grows to 3). In this way the process continues. At the end of the fourth walk, the front and back doors contain 0 and 4 pairs of shoes, respectively. Unfortunately, when going for the fifth walk, Mr. A happens to choose the front door as the starting point. He then finds no shoes. The average number of finished walks when starting with four pairs of shoes is 12 (the number of finished walks was four in Snapshot 1).
Snapshot 2: The initial situation is the same as in Snapshot 1. Now, there are only the minimum number of finished walks, 2. Indeed, at the start of the first, second, and third walks Mr. A happens to choose the front door and at the end of the first and second walk he happens to stop at the back door. At the start of the third walk, he finds no shoes at the front door.
Snapshot 3: Again, the initial situation is the same as in Snapshot 1. Now Mr. A can complete 44 walks.
The average number of finished walks can be shown [1] to be 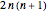 , where
, where  is the total number of pairs of shoes. So, if there are initially 1, 2, 3, …, 10 pairs of shoes at both the front and back door (that is,
is the total number of pairs of shoes. So, if there are initially 1, 2, 3, …, 10 pairs of shoes at both the front and back door (that is, 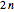 takes the values 2, 4, 6, …, 20), the average number of finished walks is 4, 12, 24, 40, 60, 84, 112, 144, 180, and 220, respectively.
takes the values 2, 4, 6, …, 20), the average number of finished walks is 4, 12, 24, 40, 60, 84, 112, 144, 180, and 220, respectively.
The Demonstration is based on [1, pp. 38–39]. A similar Demonstration is Umbrella Quandary.
Reference
[1] J. Andel, Mathematics of Chance, New York: Wiley, 2001.
Permanent Citation
"Walking Randomly Until No Shoes Are Available"
http://demonstrations.wolfram.com/WalkingRandomlyUntilNoShoesAreAvailable/
Wolfram Demonstrations Project
Published: January 27 2014