The Three-Tower Problem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
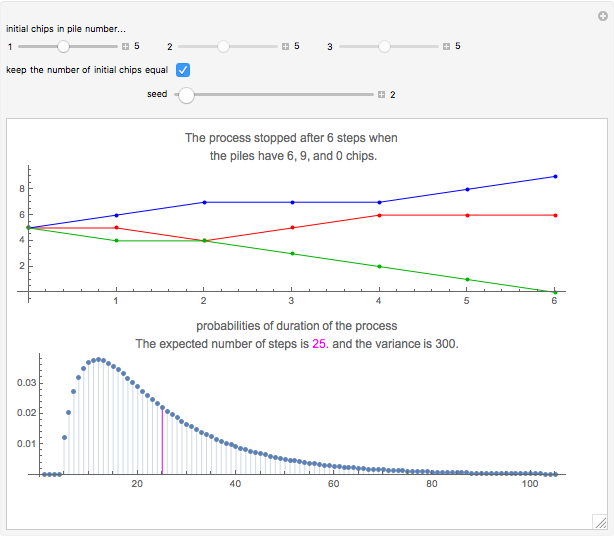
There are three piles of chips. Two piles are chosen at random and a chip is moved from the first choice to the second. This procedure is continued until one of the piles becomes empty. The Demonstration shows simulations of this process. You can see the probabilities of the duration of the process and read the expected value and variance of the duration.
Contributed by: Heikki Ruskeepää (February 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
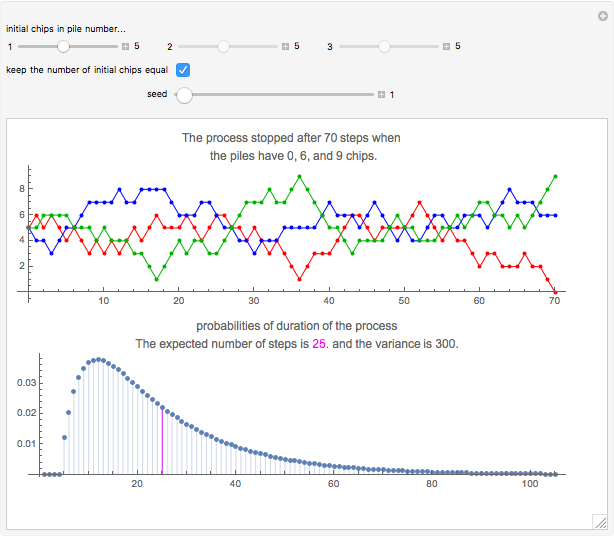
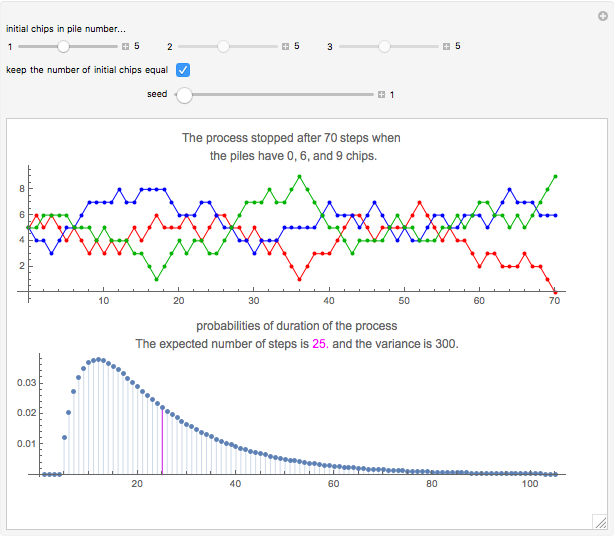
Snapshot 1: The development of the current number of chips in the three piles are shown with red, blue, and green paths. In this example, each of the three piles initially has five chips. After 70 steps, the first pile becomes empty; at this point, the other two piles have six and nine chips, respectively. When the piles initially have five chips each, the expected duration of the process is 25 and the most probable duration is 12. The duration cannot be 1, 2, 3, or 4 steps (these probabilities are zero). The process stops, with high probability, before 100 steps. However, there is no upper limit for the duration.
Snapshot 2: Here, the game only lasted six steps. The minimum number of steps is five when each pile starts with five chips.
Snapshot 3: Each pile now starts with 10 chips. The process lasted 312 steps, while the expected duration is 100. We could calculate that the probability that the game lasts at least 312 steps is 0.017.
It can be shown (see [3] and [1, pp. 39-40]), that if the piles initially have  ,
,  , and
, and  chips, the expected duration of the process is
chips, the expected duration of the process is  . For example, if
. For example, if  , the expected duration is
, the expected duration is  . The whole distribution and the mean and variance of the duration of the process is computed in [2]. For example, the probability that the duration is
. The whole distribution and the mean and variance of the duration of the process is computed in [2]. For example, the probability that the duration is  is
is
 ,
,
where 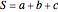 and
and  .
.
The exact general expected duration is unknown for four piles. See [2] for an explanation of why no simple solutions can be expected for four or more piles.
The three-tower process can also be interpreted as a gambler's ruin process with three gamblers, as follows. A randomly chosen gambler loses a coin and another randomly chosen gambler gets it. The game continues until one of the three gamblers is ruined. For the original gambler's ruin problem with two gamblers, see The Gambler's Ruin.
References
[1] J. Andel, Mathematics of Chance, New York: Wiley, 2001.
[2] F. T. Bruss, G. Louchard, and J. W. Turner, "On the N-Tower-Problem and Related Problems," Advances in Applied Probability, 35(1), 2003, pp. 278–294.
[3] A. Engel, "The Computer Solves the Three Tower Problem," American Mathematical Monthly, 100(1), 1993, pp. 62–64. doi:10.2307/2324818.
Permanent Citation