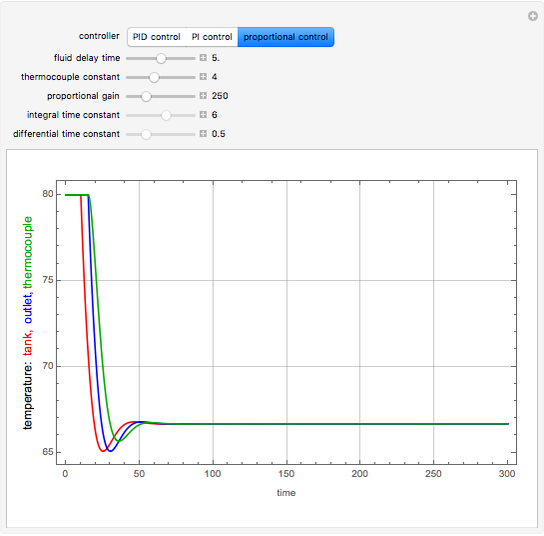
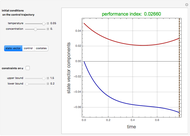
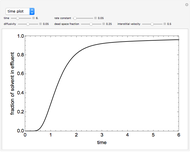
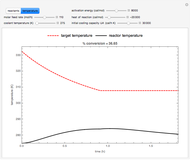
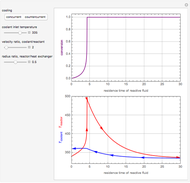
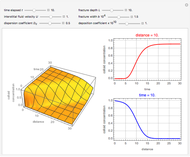
This Demonstration simulates the dynamics of a continuous process system consisting of a well-stirred tank, heater, and PID temperature controller. The liquid feed stream flows into a constant-volume heated tank at a constant rate. The outlet stream is heated to a higher set point temperature. The outlet temperature is measured by a thermocouple, while a PID temperature controller adjusts the required heater input. The objective is to maintain the outlet temperature equal to the set point whatever the change in inlet temperature. The thermocouple in the outlet stream is described by a first-order system plus dead time for the output flow to reach the measurement point.