Multiple Steady States in a Continuously Stirred Tank Reactor

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
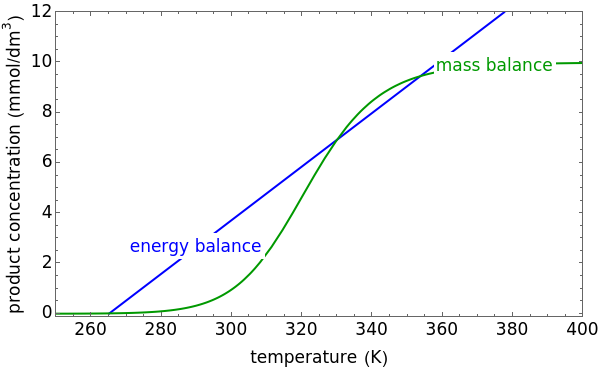
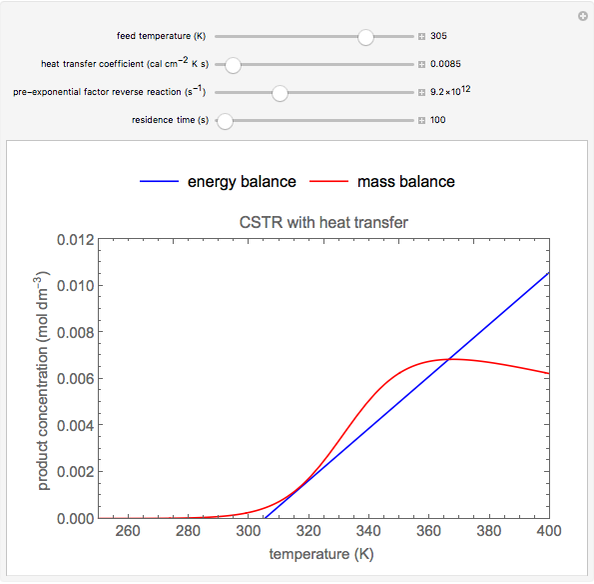
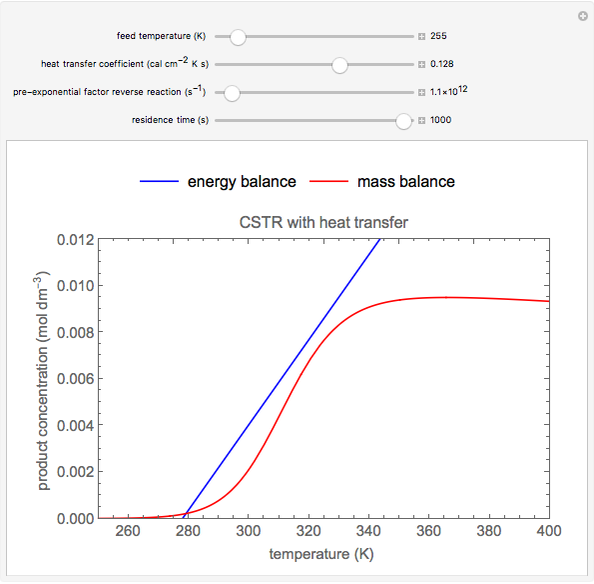
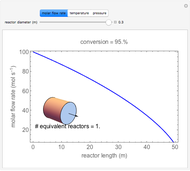
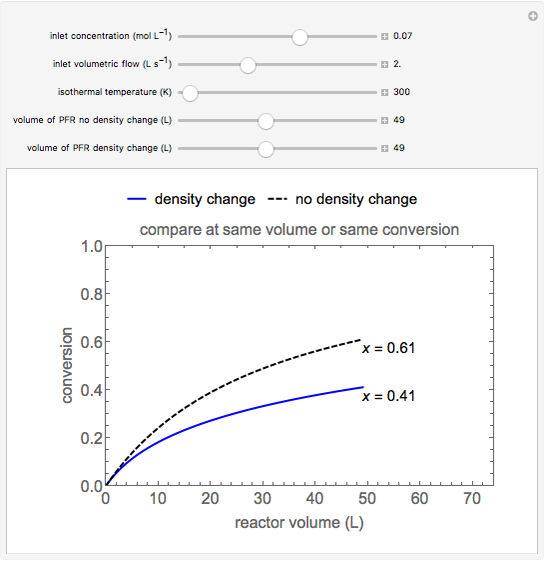
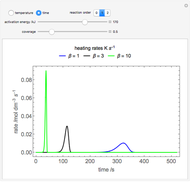
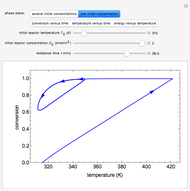
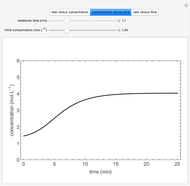
This Demonstration plots the concentration of product  as a function of temperature for the mass and energy balances done on a continuous stirred-tank reactor (CSTR) with heat transfer. The reversible, elementary, exothermic reaction
as a function of temperature for the mass and energy balances done on a continuous stirred-tank reactor (CSTR) with heat transfer. The reversible, elementary, exothermic reaction 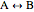 takes place in the CSTR. Use sliders to change the feed temperature, residence time, heat transfer coefficient, and reverse-reaction pre-exponential factor. The intersections of the green curve and straight blue line correspond to the steady-state solutions for the CSTR. Either one or three solutions are possible; for three solutions, the middle solution is unstable.
takes place in the CSTR. Use sliders to change the feed temperature, residence time, heat transfer coefficient, and reverse-reaction pre-exponential factor. The intersections of the green curve and straight blue line correspond to the steady-state solutions for the CSTR. Either one or three solutions are possible; for three solutions, the middle solution is unstable.
Contributed by: Rachael L. Baumann (June 2013)
Additional contributions by: John L. Falconer and Nick Bongiardina
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA
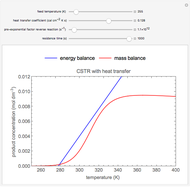
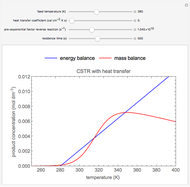
Snapshots
Details
The mass balance is nonlinear:
where 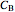 is the concentration of product
is the concentration of product 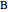 (
(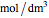 ),
), 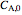 is the reactant feed concentration (mol),
is the reactant feed concentration (mol), 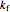 and
and 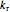 are the pre-exponential factors for the forward and reverse reactions (1/s),
are the pre-exponential factors for the forward and reverse reactions (1/s),  and
and  are the activation energies for the forward and reverse reactions (cal/mol),
are the activation energies for the forward and reverse reactions (cal/mol),  is residence time (s),
is residence time (s),  is the ideal gas constant (J/[mol K]), and
is the ideal gas constant (J/[mol K]), and 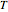 is temperature of the CSTR (K).
is temperature of the CSTR (K).
The energy balance is linear and has two terms that correspond to (1) the energy needed to change the feed temperature to the reactor temperature, and (2) the energy removed or added by heat transfer to a cooling/heating fluid, which is at a constant temperature of 310 K.
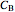 =
= 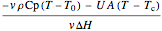 ,
,
where  is the volumetric flow rate (
is the volumetric flow rate (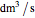 ),
),  is the density of the bulk fluid (
is the density of the bulk fluid (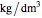 ),
), 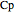 is the mass heat capacity of the feed (cal/[kg K]),
is the mass heat capacity of the feed (cal/[kg K]), 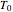 and
and  are the temperatures of the feed and coolant (K),
are the temperatures of the feed and coolant (K), 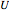 is the heat transfer coefficient (
is the heat transfer coefficient ( ),
), 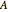 is the heat transfer area (
is the heat transfer area ( ), and
), and  is the heat of reaction (cal/mol).
is the heat of reaction (cal/mol).
As the feed temperature increases from a low value, the reactor temperature increases until the reactor reaches a temperature above which three steady-state solutions are possible. The upper and lower solutions are stable, and the middle solution is unstable. The operating conditions of the reactor depend on how the reactor is started up. As the feed temperature increases further, a temperature is reached above which only one solution is possible, and this has a high conversion.
Varying the heat transfer coefficient changes both the slope and intercept of the energy balance line, and this can change the number of steady-state solutions. Increasing the pre-exponential factor for the reverse reaction changes the mass balance curve, and the maximum conversion decreases as the equilibrium conversion become less than one.
The screencast video at [1] shows how to use this Demonstration.
Reference
[1] Multiple Steady States in a Continuously Stirred Tank Reactor. www.colorado.edu/learncheme/kinetics/MultipleSteadyStatesCSTRnoHeat.html.
Permanent Citation