Hold-or-Exercise for an American Put Option

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
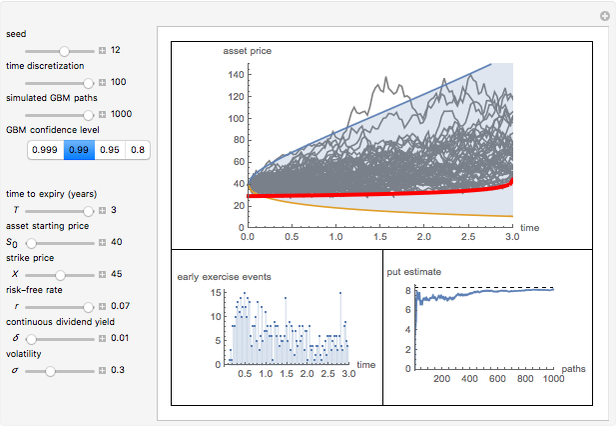
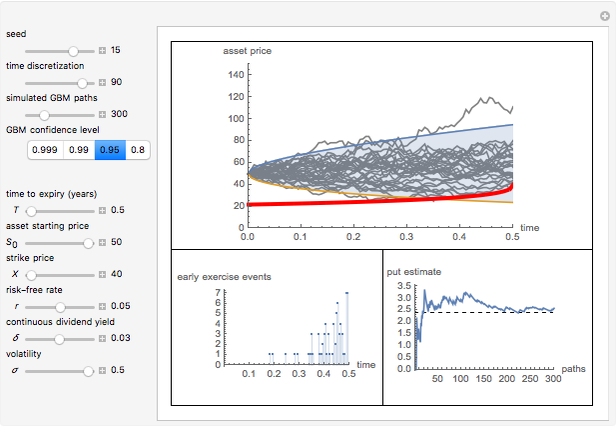
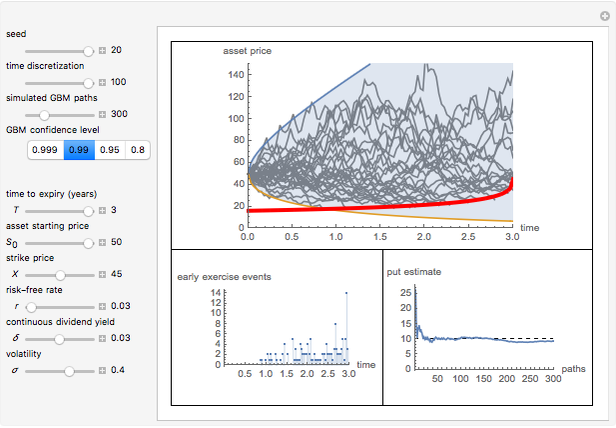
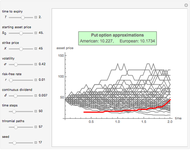
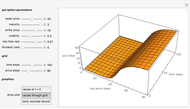
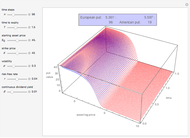
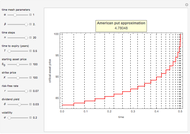
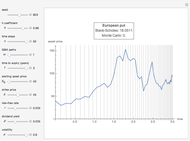
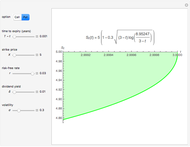
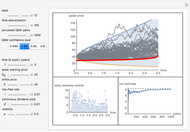
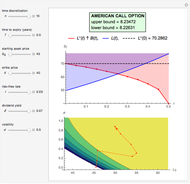
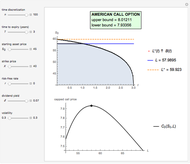
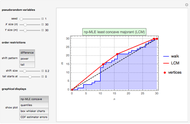
This Demonstration shows the "hold-or-exercise" process during the life of an American put option. The early exercise boundary is constructed according to the quadratic approximation analytical method [1]. Pseudorandom geometric Brownian motion (GBM) paths simulate the asset price through time; whenever a path touches the boundary (dashed red line in the upper graph), the option is instantly exercised. For each path, the intrinsic value of the option at the time of exercise is discounted, and Monte Carlo integration helps to estimate the American put at  . Use the controls to set the parameters of the option and observe the impact of time discretization and number of GBM paths on the convergence. The more GBM paths, the better the approximation.
. Use the controls to set the parameters of the option and observe the impact of time discretization and number of GBM paths on the convergence. The more GBM paths, the better the approximation.
Contributed by: Michail Bozoudis (June 2014)
Suggested by: Michail Boutsikas
Open content licensed under CC BY-NC-SA
Snapshots
Details
In the upper graph, the dashed red line represents the approximation of the early exercise boundary. It is constructed according to the quadratic approximation analytical method [1]. The light blue area shows where the asset price is expected to be in the future according to the GBM model, at the selected "GBM confidence level". Only one for every 10 GBM paths is shown in the graph.
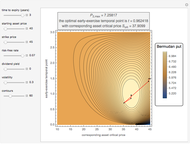
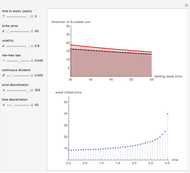
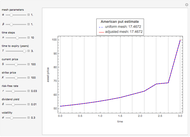
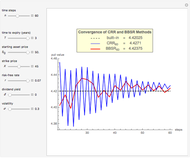
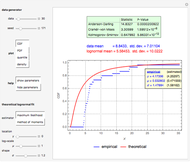
The left lower graph shows the events of early exercise per time step (before the expiry of the option) as you increase the number of GBM paths.
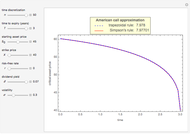
The right lower graph shows the American put convergence as you increase the number of GBM paths. The horizontal dashed black line represents the estimate of the American put at  , according to the quadratic approximation analytical method [1].
, according to the quadratic approximation analytical method [1].
Reference
[1] G. Barone–Adesi and R. Whaley, "Efficient Analytic Approximation of American Option Values," Journal of Finance, 42(2), 1987 pp. 301–320.
Permanent Citation