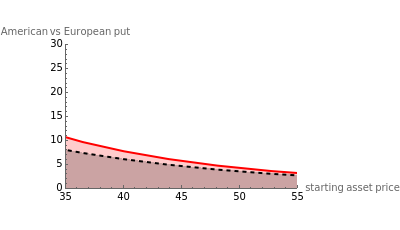
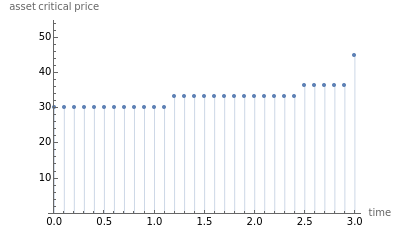
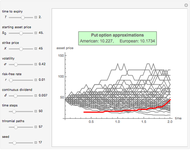
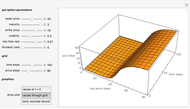
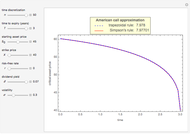
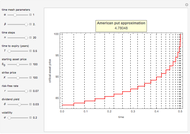
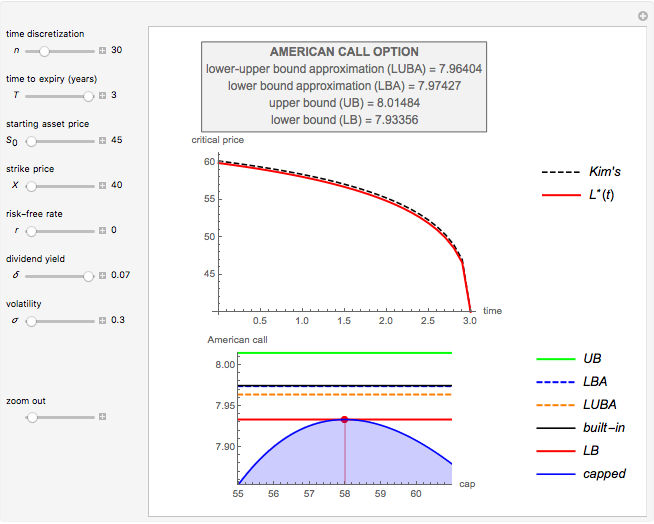
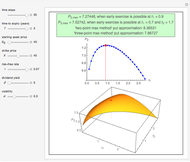
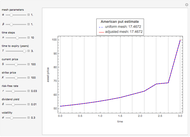
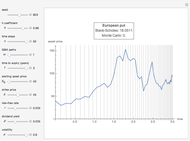
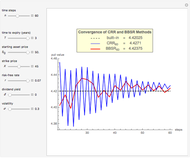
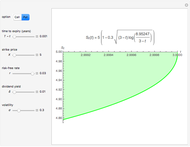
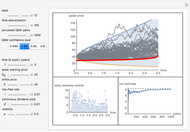
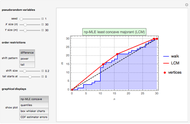
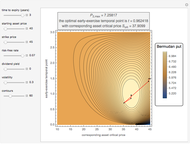
Pricing Put Options with the Implicit Finite-Difference Method
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
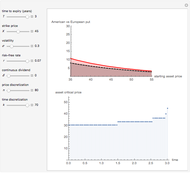
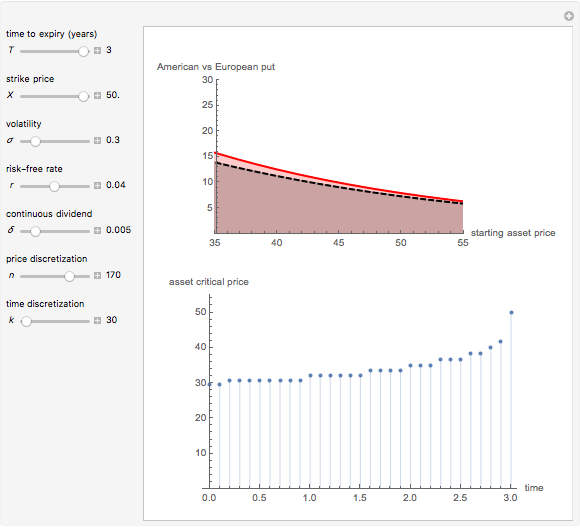
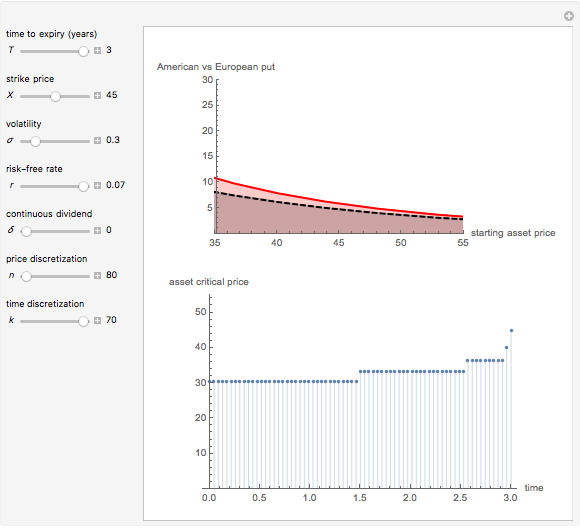
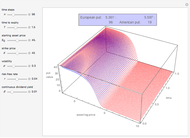
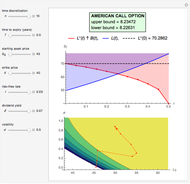
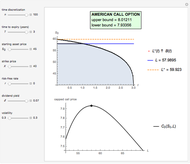
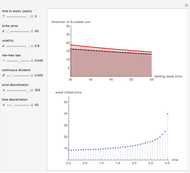
This Demonstration shows the impact of time to expiry, strike price, volatility, risk-free rate, and dividend:
[more]
Contributed by: Michail Bozoudis (June 2014)
Suggested by: Michail Boutsikas
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] M. Brennan and E. Schwartz, "Finite Difference Methods and Jump Processes Arising in the Pricing of Contingent Claims: A Synthesis", The Journal of Financial and Quantitative Analysis, 13(3), 1978 pp. 461–474.