Adaptive Mesh Relocation-Refinement (AMrR) on Kim's Method for Options Pricing

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
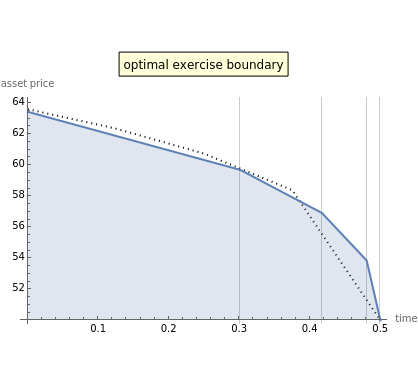
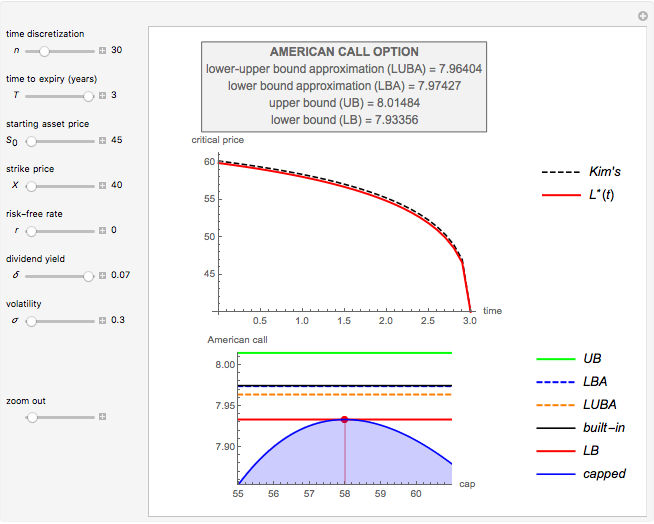
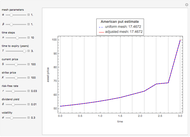
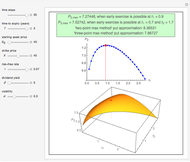
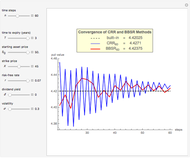
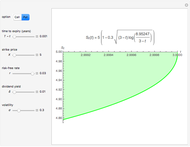
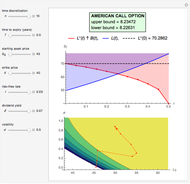
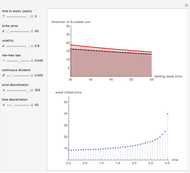
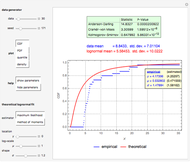
This Demonstration shows an adaptive mesh relocation-refinement (AMrR or sometimes AMR) strategy on Kim's method [1] for pricing American options, using the composite trapezoidal rule over a time mesh with four steps. A European financial option is an instrument that allows its holder the right to buy or sell an equity at a future maturity date for a fixed price called the "strike price." An American option allows its holder to exercise the contract at any time up to the maturity date, and because of this, it is worth more than the European option by an amount called the "early exercise premium." For the American call's holder, the early exercise becomes optimal when the underlying asset price exceeds a critical boundary 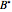 , above which the intrinsic value of the option becomes greater than its holding value. According to Kim's method, the valuation of the American option derives from an integral expression of the early exercise premium as a function of the optimal exercise boundary plus the value of the European option.
, above which the intrinsic value of the option becomes greater than its holding value. According to Kim's method, the valuation of the American option derives from an integral expression of the early exercise premium as a function of the optimal exercise boundary plus the value of the European option.
Contributed by: Michail Bozoudis (January 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
In this detailed description, the symbols have the following meanings:
 is the current time
is the current time
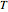 is the maturity date
is the maturity date
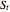 is the stock price at time
is the stock price at time 
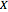 is the strike price
is the strike price
 is the stock dividend yield
is the stock dividend yield
 is the risk-free interest rate
is the risk-free interest rate
 is the stock volatility
is the stock volatility
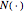 is the cumulative distribution function of the standard normal distribution
is the cumulative distribution function of the standard normal distribution
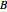 is the moving free boundary
is the moving free boundary
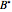 is the optimal boundary.
is the optimal boundary.
Consider the class of contracts consisting of a European call option and a sure flow of payments that are paid at the rate
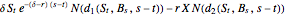
for  ,
,
where
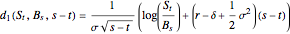 ,
,
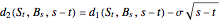 ,
,
and 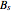 is a non-negative continuous function of time. Each member of the class of contracts is parametrized by
is a non-negative continuous function of time. Each member of the class of contracts is parametrized by 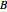 . The value of the contract at time
. The value of the contract at time  is
is
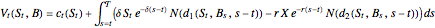 ,
,
where 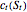 denotes the value at time
denotes the value at time  of a European call option on
of a European call option on 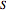 with strike price
with strike price 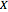 and maturity
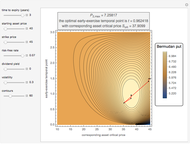
and maturity 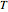 . The optimal exercise boundary
. The optimal exercise boundary 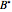 for the American call option is obtained by solving the value matching condition:
for the American call option is obtained by solving the value matching condition:
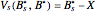 ,
,
for 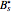 for all
for all 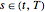 .
.
The value of the American call option 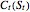 is then given by
is then given by 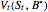 .
.
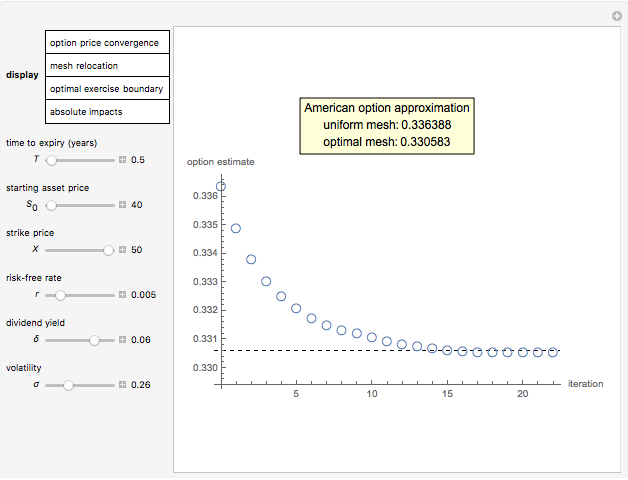
Subject to the value matching condition, the critical asset price at time  can be numerically approximated by a computationally intensive recursive procedure. This method requires solving
can be numerically approximated by a computationally intensive recursive procedure. This method requires solving  integral equations, where
integral equations, where  is the number of time steps. Each time the integral equation is solved, either the trapezoidal rule (Wolfram MathWorld) or Simpson's rule (Wolfram MathWorld) can be employed to approximate the integral.
is the number of time steps. Each time the integral equation is solved, either the trapezoidal rule (Wolfram MathWorld) or Simpson's rule (Wolfram MathWorld) can be employed to approximate the integral.
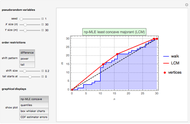
For the mesh relocation process, the following notation is used:
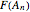 : an invertible mesh function that maps the arbitrary set
: an invertible mesh function that maps the arbitrary set 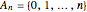 in the computational space
in the computational space 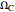 , to a set
, to a set  in the physical time domain
in the physical time domain  , where
, where  and
and 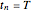 .
.
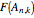 : an invertible mesh function that maps the arbitrary set
: an invertible mesh function that maps the arbitrary set 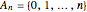 to a set
to a set 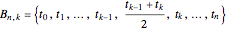 ,
, 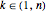 .
.
 : a scalar function that uses Kim's method to approximate the American call value at
: a scalar function that uses Kim's method to approximate the American call value at  , over the mesh mapping function
, over the mesh mapping function  .
.
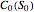 : the theoretical value of the American call at
: the theoretical value of the American call at  .
.
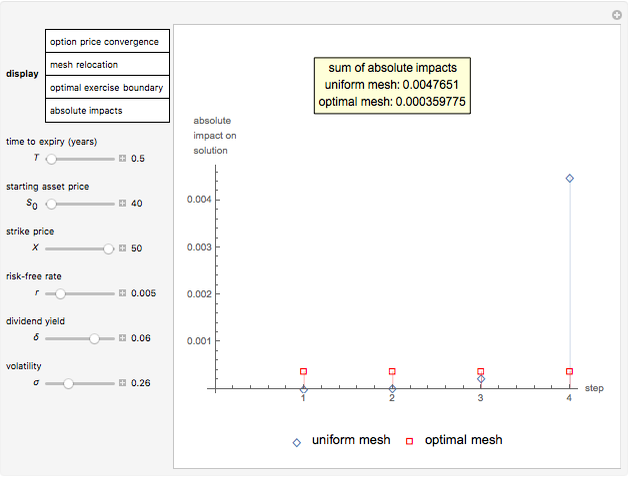
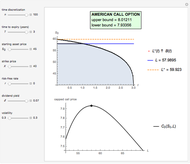
 : the impact of the
: the impact of the 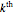 element's local refinement on the solution. Every element's impact on the solution is evaluated as it gets divided into two equal subintervals, while all other elements remain unchanged.
element's local refinement on the solution. Every element's impact on the solution is evaluated as it gets divided into two equal subintervals, while all other elements remain unchanged.
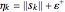 : the absolute impact of the
: the absolute impact of the 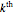 element's local refinement on the solution. A small positive real
element's local refinement on the solution. A small positive real 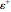 is added to ensure that
is added to ensure that 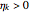 .
.
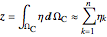 : the adjoint functional derives as the sum of absolute impacts and serves as the dual-objective quantity under minimization.
: the adjoint functional derives as the sum of absolute impacts and serves as the dual-objective quantity under minimization.
The minimization of  requires that
requires that 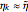 ,
, 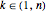 . Hence, the
. Hence, the 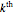 element should be resized according to the ratio
element should be resized according to the ratio 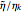 . In order to run a smooth element resizing process, a weight
. In order to run a smooth element resizing process, a weight  is introduced:
is introduced:
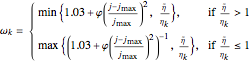
where  is a restrictive parameter that controls the variability in
is a restrictive parameter that controls the variability in  , and
, and 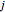 is the iteration index (this Demonstration uses
is the iteration index (this Demonstration uses  ,
,  and
and 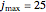 ). Through every iteration, all mesh points are relocated simultaneously; the new position
). Through every iteration, all mesh points are relocated simultaneously; the new position 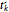 of the temporal point
of the temporal point 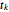 is obtained by
is obtained by 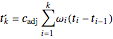 , where
, where  is an adjusting coefficient to ensure that
is an adjusting coefficient to ensure that 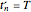 . The refinement process is terminated when
. The refinement process is terminated when 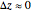 or
or 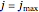 .
.
References
[1] I. J. Kim, "The Analytic Valuation of American Options," The Review of Financial Studies, 3(4), 1990 pp. 547–572. www.jstor.org/stable/2962115.
[2] A. Ern, S. Villeneuve and A. Zanette, "Adaptive Finite Element Methods for Local Volatility European Option Pricing," International Journal of Theoretical and Applied Finance, 7(6), 2004 pp. 659–684. doi:10.1142/S0219024904002669.
[3] C. Goll, R. Rannacher and W. Wollner, "The Damped Crank–Nicolson Time-Marching Scheme for the Adaptive Solution of the Black–Scholes Equation," Journal of Computational Finance, 18(4), 2015 pp. 1–37. doi:10.21314/JCF.2015.301.
[4] J. T. Oden and S. Prudhomme, "Goal-Oriented Error Estimation and Adaptivity for the Finite Element Method," Computers and Mathematics with Applications, 41(5–6), 2001 pp. 735–756. doi:10.1016/S0898-1221(00)00317-5.
[5] K. G. van der Zee, E. H. van Brummelen and R. de Borst, "Goal-Oriented Error Estimation and Adaptivity for Free-Boundary Problems: The Domain-Map Linearization Approach," SIAM Journal on Scientific Computing, 32(2), 2010 pp. 1064–1092. doi:10.1137/080741227.
[6] P. Luchini, F. Giannetti and V. Citro, "Error Sensitivity to Refinement: A Criterion for Optimal Grid Adaptation," Theoretical and Computational Fluid Dynamics, 2016. doi:10.1007/s00162-016-0413-x.
[7] M. Broadie and J. Detemple, "American Option Valuation: New Bounds, Approximations, and a Comparison of Existing Methods," The Review of Financial Studies, 9(4), 1996 pp. 1211–1250. doi:10.1093/rfs/9.4.1211.
[8] S.-L. Chung, M.-W. Hung, and J.-Y. Wang, "Tight Bounds on American Option Prices," Journal of Banking and Finance, 34(1), 2010 pp. 77–89. doi:10.1016/j.jbankfin.2009.07.004.
Permanent Citation