SARIMA Process Forecasting Model

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
This Demonstration applies the Wolfram Language's built-in function SARIMAProcess to construct a forecasting SARIMA (seasonal autoregressive integrated moving average) model based on Monte Carlo simulation.
Contributed by: Michail Bozoudis (August 2014)
Suggested by: Michail Boutsikas
Open content licensed under CC BY-NC-SA
Snapshots
Details
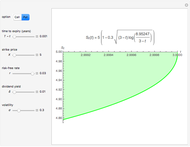
Suppose that you have identified a SARIMA process 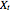 , after the analysis of historical data [1], [2]. You can adjust the sliders to the coefficients' specific values, integration orders (differencing), seasonal order, and white noise (
, after the analysis of historical data [1], [2]. You can adjust the sliders to the coefficients' specific values, integration orders (differencing), seasonal order, and white noise (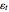 ) variance; then, select the number of pseudorandom SARIMA paths and the number of future periods (T) to predict. The more SARIMA paths, the better the approximation, but this will require more computational effort.
) variance; then, select the number of pseudorandom SARIMA paths and the number of future periods (T) to predict. The more SARIMA paths, the better the approximation, but this will require more computational effort.
You can choose among four display sets:
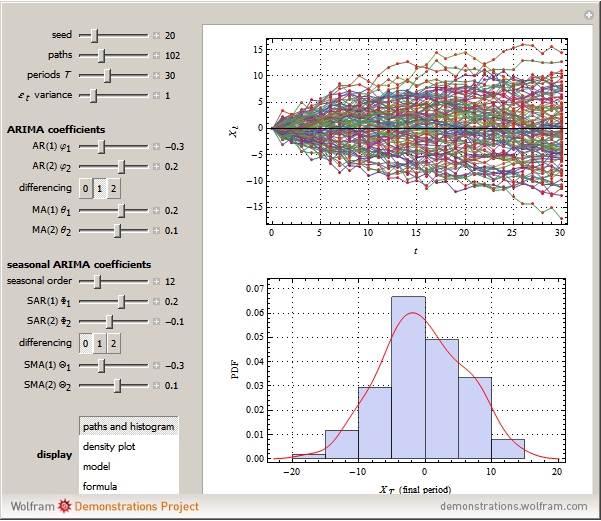
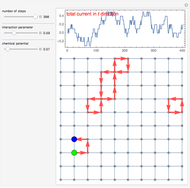
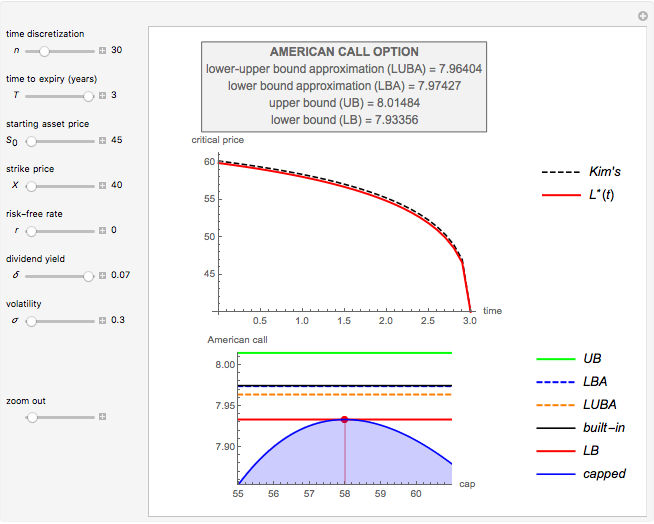
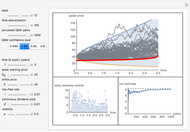
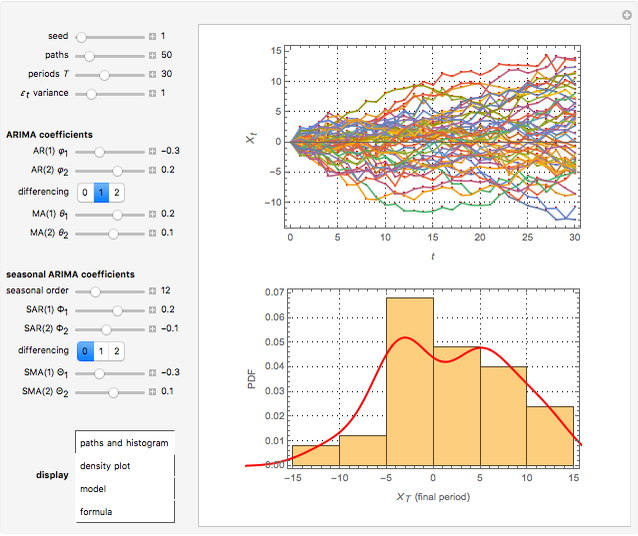
1st display set: The upper graph shows the simulation process as a bundle of SARIMA paths, from t=1 to T. The histogram shows the probability density function (PDF) for 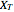 . Use the "seed" control to generate new pseudorandom SARIMA paths.
. Use the "seed" control to generate new pseudorandom SARIMA paths.
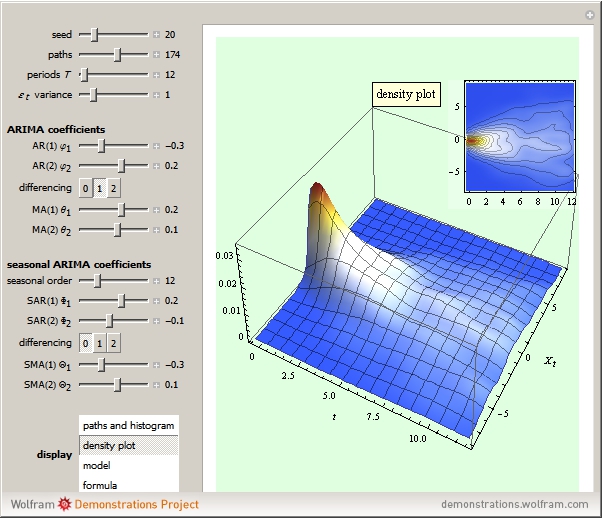
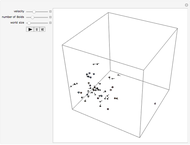
2nd display set: The 3-D plot and its 2-D epilogue illustrate the density of the SARIMA paths bundle.
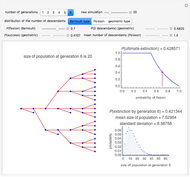
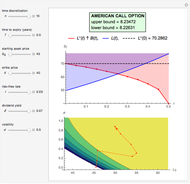
3rd display set: Shows the 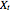 expectation algorithm according to the selected SARIMA model.
expectation algorithm according to the selected SARIMA model.
4th display set: Calculates the 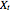 expectation formula according to the selected coefficients' specific values, integration orders, and seasonal order.
expectation formula according to the selected coefficients' specific values, integration orders, and seasonal order.
References
[1] G. E. P. Box and G. M. Jenkins, "Time Series Analysis, Forecasting and Control", Holden-Day, 1970, San Francisco.
[2] P. Newbold, "The Principles of the Box-Jenkins Approach", Operational Research Quarterly, 26(2), 1975 pp. 397–412.
Permanent Citation